- Espacio cociente
-
Espacio cociente
En álgebra lineal, el concepto del espacio cociente es de gran importancia para la álgebra de conjuntos.
Contenido
Definición
Sea E un espacio vectorial sobre el campo K, y sea N un sub espacio vectoral de V, podemos definir una relación de equivalencia entre los elementos de E “vectores”, el espacio cociente de V es el conjunto de todas las clases de equivalencia de E.
El espacio cociente es el conjunto de las clases de equivalencia sobre el “E”, la multiplicación y la suma son definidas dentro de una clase de equivalencia como:
- Suma de clases:
[u] + [v] = [u + v]
Si suponemos u + v i u1 + v1 equivalentes módulo F
(u + v) − (u1 + v1) є F
por tanto tenemos que [u] = [u1] y [v] = [v1]
ademas [u] = [0], por tanto u − 0 є F, con lo que u є F
- Producto por escalar:
u − u1 є F
k(u − u1) є F
ku − ku1 є F
por tanto [ku] = [ku1]
Clase de un vector
Siendo F un subespacio vectorial de E, diremos que u,v є E están relacionados por módulo F si
u-v є F y E/F sera su conjunto cociente.
La clase [u] de un vector u є E se define como: [u]={u+v / v є F}=u+F
Tiene las operaciones suma de clases y producto por escalar bien definidas, determinando que E/F es un subespacio de de los Reales.
Dimensión del espacio cociente
Diremos que si la dimensión de E es finita E/F también lo es, siendo dimE/F=dimE-dimF
- Demostración:u1,...,um base de F, se puede completar la base hasta obtener una de E por la ley de Steinitz u1,...,um,um + 1,...,un.
[u1] = ... = [um] = [0] ya que u1,...,um є F
por tanto tenemos que [um + 1],...,[un] podría ser la base de E/F
para funcionar como base deberán ser linealmente independientes y generadores del subespacio:
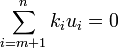
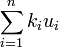є F por tanto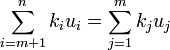 
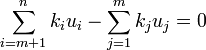con lo que ki = 0, por tanto son linealmente independientesu є E
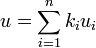
si aplicamos las clases
![[u]=[\sum_{i=1}^n k_i u_i]=\sum_{i=1}^n k_i [u_i]](/pictures/eswiki/49/1eac95aed733676a6ca9c32e39620a0d.png)
y como u1,...,um base de F, 
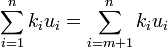
Por tanto dimE=dimF+dimE/F siendo dimE=n, dimF=m y dimE/F=n-m
Ejemplo
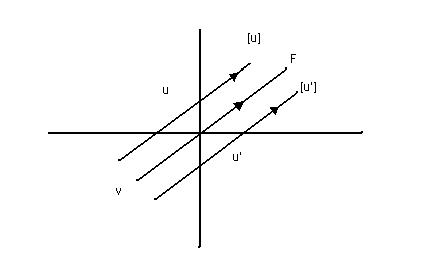
Si tenemos un subespacio F en el espacio de los Reales bidimensionales y está generado por un vector v, F=<v> la clase de un vector u contenido en R² será:
[u]={u+v / v є F}, siendo su espacio cociente R²/F={[u]}, es decir todos los vectores paralelos a F.
Categoría: Álgebra lineal
Wikimedia foundation. 2010.
