- Espacio proyectivo complejo
-
Espacio proyectivo complejo
En matemáticas, llamamos espacio proyectivo complejo al espacio de las líneas complejas de Cn+1 que pasan por el origen. Normalmente se nota por P(Cn+1), Pn(C) o CPn
Constituye una variedad compleja compacta de dimensión compleja n definida identificando los puntos proporcionales de Cn+1-{0} mediante la siguiente relación de equivalencia:
Contenido
Topología
Sea
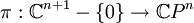 la proyección que lleva cada z en su clase de equivalencia. Dotamos a CPn de la topología cociente, de modo que
la proyección que lleva cada z en su clase de equivalencia. Dotamos a CPn de la topología cociente, de modo que  es abierto si y sólo si π − 1(U) lo es. Esta topología convierte a la proyección en una aplicación continua.
es abierto si y sólo si π − 1(U) lo es. Esta topología convierte a la proyección en una aplicación continua.- CPn es compacto y conexo
Para ello basta observar que es imagen por una aplicación continua de la esfera real S2n+1. En concreto por la composición de aplicaciones
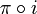 dada por
dada por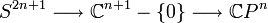 ,
,
Esta aplicación es sobreyectiva pues toda línea pasa por un punto de S2n+1.
Estructura compleja
Podemos construir un atlas mediante las cartas (Ui,Φi) definidas por:
donde por ^ debemos entender que no aparece la entrada correspondiente.
Si
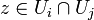 , se comprueba que el cambio de cartas
, se comprueba que el cambio de cartas 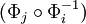 es holomorfo.
es holomorfo.Subespacios lineales de CPn
Toda inclusión del tipo Ck+1 → Cn+1 induce una inclusión entre los proyectivos correspondientes CPk → CPn. A la imagen de esta aplicación se le denomina subespacio lineal de CPn.
Si k = n-1, a la imagen de esta aplicación se le denomina hiperplano de CPn. Si k = 1, de su imagen se dice que es una línea del mismo.
Referencias
- P. Griffiths y J. Harris. Principles of algebraic geometry. John Wiley & Sons, 1978. ISBN 0-471-32792-1 . (Cap. 2)
Véase también
- Espacio proyectivo real
- Espacio proyectivo cuaterniónico
- Geometría algebraica
Categorías: Variedades complejas | Geometría proyectiva | Variedades algebraicas
Wikimedia foundation. 2010.

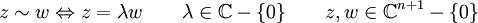
![U_i=\{[z]:z \in \mathbb{C}^{n+1}-\{0\}, z_i \neq 0\} \qquad \Phi_i([z])=(\frac {z_0}{z_i},\cdots,\hat\frac {z_i}{z_i},\cdots,\frac {z_n}{z_i})](/pictures/eswiki/98/be00816b7a7d53f06e4a87b43bff6cda.png)