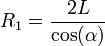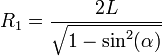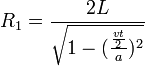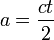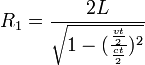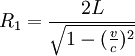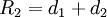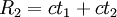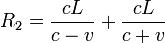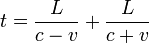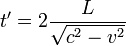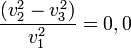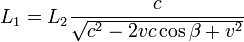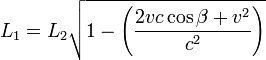- Experimento de Michelson y Morley
-
Experimento de Michelson y Morley
El experimento de Michelson y Morley fue uno de los más importantes y famosos de la historia de la física. Realizado en 1887 por Albert Abraham Michelson y Edward Morley, está considerado como la primera prueba contra la teoría del éter. El resultado del experimento constituiría posteriormente la base experimental de la teoría de la relatividad especial de Einstein.
Motivación
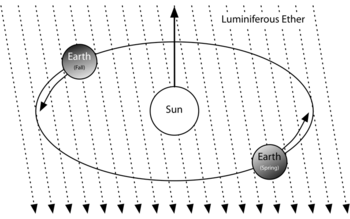
La teoría física del final del siglo I postulaba que, al igual que las olas y el sonido son ondas que necesitan un medio para transportarse (como el agua o el aire), la luz también necesitaría un medio, llamado "éter". Como la velocidad de la luz es tan grande, diseñar un experimento para detectar la presencia del éter era muy difícil.
El propósito de Michelson y Morley era medir la velocidad relativa a la que se mueve la Tierra con respecto al éter.
Cada año, la Tierra recorre una distancia enorme en su órbita alrededor del Sol, a una velocidad de 30 km/s (más de 100.000 km/h). Se creía que la dirección del "viento del éter" con respecto a la posición de nuestra estrella variaría al medirse desde la Tierra, y así podría ser detectado. Por esta razón, y para evitar los efectos que podría provocar el Sol en el "viento" al moverse por el espacio, el experimento debería llevarse a cabo en varios momentos del año.
El efecto del viento del éter sobre las ondas de luz, sería como el de la corriente de un río sobre un nadador que se mueve a favor o en contra de ella. En algunos momentos el nadador sería frenado, y en otros impulsado. Esto es lo que se creía que pasaría con la luz al llegar a la Tierra con diferentes posiciones con respecto al éter: debería llegar con diferentes velocidades. La clave es que, en viajes circulares, la diferencia de velocidades es muy pequeña, del orden de la millonésima de la millonésima de un segundo. Sin embargo, Michelson, muy experimentado con la medición de la velocidad de la luz, ideó una manera de medir esta mínima diferencia.
Descripción del experimento
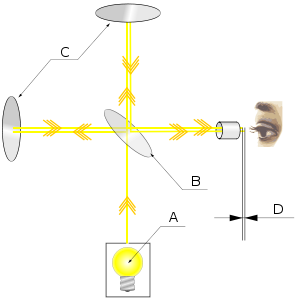
 Esquema del interferómetro de Michelson (aunque utilizando un láser).
Esquema del interferómetro de Michelson (aunque utilizando un láser).
En la base de un edificio cercano al nivel del mar, Michelson y Morley construyeron lo que se conoce como el interferómetro de Michelson. Se compone de una lente semiplateada o semiespejo, que divide la luz monocromática en dos haces de luz que viajan en un determinado ángulo el uno respecto al otro.
Con esto se lograba enviar simultáneamente dos rayos de luz (procedentes de la misma fuente) en direcciones perpendiculares, hacerles recorrer distancias iguales (o caminos ópticos iguales) y recogerlos en un punto común, en donde se crea un patrón de interferencia que depende de la velocidad de la luz en los dos brazos del interferómetro. Cualquier diferencia en esta velocidad (provocada por la diferente dirección de movimiento de la luz con respecto al movimiento del éter) sería detectada.
Descripción, de manera esquemática, de como se desarrolló este experimento:
La distancia entre los espejos y el semiespejo tiene una longitud "L", es decir, el "Recorrido 1" es igual al "Recorrido 2".
Existe una diferencia entre los recorridos 1 y 2 observados en la Tierra y fuera de la Tierra (observador externo). Los recorridos para el observador externo (fuera del planeta), el cual está en reposo, serán:
Como:
Se tiene entonces que:
Finalmente, obtenemos después de simplificar, que el Recorrido 1 es igual a:
Para obtener el Recorrido 2 se tiene lo siguiente (Ver Figura 3):
Para hallar t1 y t2 se puede suponer que a la ida (t1) la luz va a una velocidad c-v y la distancia sigue siendo L, e igualmente para la vuelta (t2) se puede suponer que la velocidad es c+v y la distancia L. Entonces se tiene que: t1=l/(c-v) y t2=l/(c+v):
- El tiempo empleado por el barco a favor de la corriente y contra corriente, según la interpretación de Michelson y Morley, estaría dado por:
- El tiempo empleado por el barco que se desplaza en ángulo recto, para Michelson y Morley es:
- La diferencia en el tiempo sería:
-
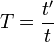 =
=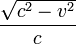
- La contracción de Lorentz es una consecuencia de las fórmulas matemáticas señaladas anteriormente. Contracción que está representada por la siguiente expresión:
-
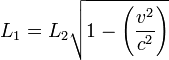 ,
,
donde L1 es la distancia medida por un observador estacionario y L2 es la distancia medida por un observador que se desplaza a una velocidad v siendo c la velocidad de la luz. Y para el caso del interferómetro, en examen, la contracción correspondería a la reducción de la longitud de uno de sus brazos, lo que explicaría el motivo por el cuál ambos haces de luz llegaron simultáneamente a su destino (llegaron en fase).
La analogía usada por Michelson y Morley se refiere a dos barcos, un río y un observador.
Experimentos realizados hasta 1930
Investigador Año del experimento Metros de cada Brazo del Interferómetro L1 y L2 Corrimiento de franja predicho Límite superior del corrimiento observado Lugar Upper Limit on Vaether Predicho
v/s
Observado
%Obser. Michelson 1881 1.2 0.04 0.02 Potsdam 50% (A) Michelson y Morley 1887 11.0 0.04 < 0.01 Cleveland 8 km/s 25% (B) Morley y Miller 1902–1904 32.2 1.13 0.015 Cleveland 1,33% Miller 1921 32.0 1.12 0.08 Mt. Wilson 7,14% Miller 1923–1924 32.0 1.12 0.03 Cleveland 2,68% Miller (luz solar) 1924 32.0 1.12 0.014 Cleveland 1,25% Tomascheck (luz estelar) 1924 8.6 0.3 0.02 Heidelberg 6% Miller 1925–1926 32.0 1.12 0.088 Mt. Wilson 7,86% Kennedy (Mt Wilson) 1926 2.0 0.07 0.002 Pasadena y Mt. Wilson 2,85% Illingworth 1927 2.0 0.07 0.0002 Pasadena 1 km/s 0,285% Piccard y Stahel (Rigi) 1927 2.8 0.13 0.006 Mt. Rigi 4,62% Michelson y colaboradores 1929 25.9 0.9 0.01 Mt. Wilson 1,12% Joos 1930 21.0 0.75 0.002 Jena 0,267% - (A) En el año 1851 ya se había predicho por Fizeau, con motivo del resultado entregado por su "interferómetro" con agua como medio, un resultado que concordaba, más o menos, en un 56,5% con una de las teorías y en un 43,5% con la otra, esto es, con la teoría del éter estático no arrastrado por el agua, y con del éter arrastrado por el agua.
- (B) Michelson y Morley en el año 1887, cuyo "interferometro" con aire como medio, pudieron obtener una longitud de trayectoria óptica ( L1 + L2 ) de cerca de 22 metros. En ese experimento la longitud de cada brazo del interferómetro fue de 11 metros.
-
- De manera que ΔN = ( 2 L / λ )
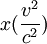 si se escoge λ = 5,5 x
si se escoge λ = 5,5 x 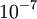 y
y 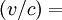
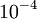 , entonces la ecuación es:
, entonces la ecuación es:
- De manera que ΔN = ( 2 L / λ )
-
- ΔN =
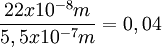
- ΔN =
Si la diferencia de trayectoria óptica —que hay entre los haces en el Interferómetro de Michelson— varía en una distancia igual a la longitud de onda, entonces, una raya o franja habrá de trasladarse a través del retículo de la mirilla de observador. Si ΔN representa el número de franjas que pasan por el retículo, a medida que el espectro se corre, y si se utiliza luz de longitud de onda λ, de modo que el período de una vibración sea T = 1 / v = λ / c, entonces:
-
- ΔN =
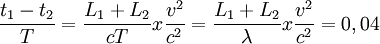
- ΔN =
Si se varía la longitud de algunos de los caminos ópticos del interferómetro (la longitud de uno de los brazos del instrumento), las franjas de interferencia se mueven a través de la pantalla a medida que en cada punto las ondas se refuerzan y anulan sucesivamente. Por ello, el aparato estacionario no nos puede decir nada referente a diferencias de tiempo en el recorrido de los dos caminos (los brazos del interferómetro). Sin embargo, si se gira el aparato 90º, los dos caminos cambian su orientación con respecto a la hipotética corriente de éter, de tal manera que el rayo que antes necesitaba un tiempo t 1 para el recorrido total, requiere ahora un tiempo t 2 y viceversa. Si estos tiempos son diferentes, las franjas se moverán a través de la pantalla durante el giro.
En donde v es la velocidad del éter que tomaremos igual a la velocidad de rotación de la tierra en su orbita de valor 3 x 104 m/s y c es la velocidad de la luz de valor 3 x 108 m/s
Como el desplazamiento de franjas de interferencia se verifica en ambos recorridos, el desplazamiento total debería ser de 2N o sea 0,04 franjas. Un desplazamiento de esta magnitud es fácilmente observable, y en consecuencia Michelson y Morley tenían esperanza de demostrar directamente la existencia del éter.
- Ante la sorpresa general, no se detectó absolutamente ningún desplazamiento de franjas de interferencia.
- Los resultados del experimento ya singularizado se interpretaron de tal forma que se concluyó:
-
-
- El éter carecía de propiedades inmedibles resultando, como consecuencia directa de aquello, que la hipótesis del éter era insostenible.
-
-
-
- Se vislumbraba el nacimiento de nuevos principios para física: la contracción de la longitud; la dilatación del tiempo; y una constante universal.
-
El experimento fallido menos famoso de la historia
Irónicamente, tras toda esta preparación, el experimento fue fallido, aunque exitoso. En vez de mostrar las propiedades del éter, no se produjo ninguna alteración de velocidad de la luz y, por tanto, ninguno de los efectos que el "viento del éter" tenía que producir. El aparato se comportó como si no hubiese "viento del éter". Este asombroso resultado no podía ser explicado por la teoría de las ondas vigente en la época. Se intentaron muchas explicaciones, como que la Tierra arrastraba de alguna forma al propio éter, pero todas ellas resultaron ser incorrectas.
Ernst Mach fue uno de los primeros físicos en considerar que el resultado del experimento era correcto y sugirió una nueva teoría. Las investigaciones iniciadas a raíz del experimento llevaron a una teoría alternativa consistente, la contracción de Lorentz, que explicaba el resultado nulo obtenido. El desarrollo de esta teoría desembocó en la relatividad especial de Einstein.
Argumentos en contra de la interpretación asignada
Los detractores sostienen que es errónea la interpretación asignada al resultado entregado por el experimento realizado por Michelson y Morley, para lo cual, entre otras cosas, se remiten y analizan La analogía usada por Michelson y Morley
La luz se desplaza en varios medios materiales; uno de esos medios es el aire atmosférico que viaja adosado a la Tierra. En ambos brazos del interferómetro de Michelson y Morley, la luz, se desplazó a través del aire atmosférico que estaba en todas partes del instrumento; medio, que al estar adosado a la Tierra, viaja a la misma velocidad que este planeta, lo que implica que todos los eventos - en relación con el experimento realizado por Michelson y Morley - sucedieron en el mismo sistema inercial. Y sabido es, que «Ningún experimento mecánico, efectuado totalmente dentro de un sistema inercial, puede indicarle al observador cuál es el movimiento de dicho sistema con respecto a cualquier otro sistema inercial», excepto con un péndulo o con un giroscopio
En ese interferómetro se utilizaron dos haces de luz que se desplazó, no a través del vacío sino del aire, dos trayectorias ópticas distintas, determinadas por un sistema de espejos y placas que, finalmente, convergen para formar un patrón de interferencia, por causa de la diferencia de la velocidad.
Aquí no se está hablando de la Velocidad de la luz en un medio material, ni tampoco del Índice de refracción, sino de otro evento muy diferente. En efecto, se está diciendo que si el observador, como el instrumento de medición, se encuentra ubicado dentro del mismo sistema de referencia que tiene el medio en el que se desplaza la luz (Por ejemplo: el aire atmosférico), acontecerá que, ese observador, no se percatará de la velocidad de desplazamiento del medio.
Por lo tanto, si los haces de luz viajaron por el aire, resulta incorrecto utilizar la velocidad de la luz en el vacío c, ya que, en tal caso se debe usar la velocidad de la luz en el aire v. En donde, para el observador terrestre:
-
-
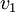 = velocidad de la luz en el aire.
= velocidad de la luz en el aire.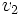 = velocidad del planeta Tierra.
= velocidad del planeta Tierra.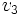 = velocidad del instrumento.
= velocidad del instrumento.
-
En tales condiciones, la velocidad de la luz, en el medio “aire”, siempre será la misma, cualquiera que sea la dirección y sentido en el que, los haces de luz, se desplacen en cada brazo del interferómetro, lo que impide detectar la supuesta “variación de velocidad” que Michelson y Morley equivocadamente supusieron podrían medir con su instrumento. En dicho experimento, la luz, viajó por el aire adosado a la Tierra, y no por el Éter, que a aquellos investigadores les permitiría visualizar la adición de velocidades, o la diferencia de velocidad que la luz tendría en cada brazo del interferómetro.
- Los detractores de Michelson y Morley, sostienen que por causa del aire presente en el instrumento, el tiempo empleado por ambos haces de luz siempre será el mismo, aún cuando uno se desplace ida y vuelta con un ángulo igual de 90º, y en donde el otro, en la ida viaje con un ángulo de 0º y luego vuelva con un ángulo de 180º), considerando - según aquellos opositores a la interpretación de los resultados provenientes de La analogía usada por Michelson y Morley (se refiere a dos barcos, un río y un observador)- se debiera aplicar la siguiente fórmula matemática, porque ella reflejaría con mayor precisión la realidad:
- Tanto para t' como para t =
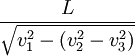
- Entonces, para dichos detractores, las franjas de interferencia estaría dado por la siguiente fórmula:
-
- ΔN =
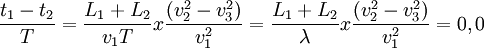
- ΔN =
 Fig. 1 - Notaciones habituales en un triángulo cualquiera.
Fig. 1 - Notaciones habituales en un triángulo cualquiera.
- Y agregan, que de ser correcta la interpretación entregada al resultado del experimento realizado por los diferentes investigadores, acontecerá que para cualquier ángulo que adopte un brazo (L1 ) del interferómetro con respecto del otro (L2 ) - por aplicación de la teorema del coseno - la fórmula más adecuada y concordante con tal interpretación, será:
-
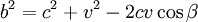 .
.
-
- t' + t =
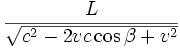 +
+ 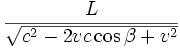
- t' + t =
(En donde el valor del ángulo beta (Δβ) es diferente para cada fracción)
- En cuanto a la contracción de Lorentz sostienen que de ser efectiva ella debiera estar en función del ángulo en los cuales se sitúe un brazo con respecto del otro, que puede ser cualquiera de la gama angular de 0º a 360 º, pasando por el ángulo de 90º con el cual se efectuó el experimento.
-
-
- Fórmula válida, exclusivamente para 90º grados, en la contracción de Lorentz:
-
-
-
- Fórmula aplicable para cualquier ángulo, en la contracción de Lorentz:
-
Hipótesis contrarias
Las hipótesis propuestas por los detractores son:
- ¿Es errónea la interpretación que se asignó al resultado entregado por el interferómetro de Michelson y Morley.?
- ¿A menor densidad del medio material en que se propaga la luz, menor es el porcentaje de Fizeau?
- ¿A mayor densidad del medio material en que se propaga la luz, menor cantidad de "materia oscura fría" presente en los espacios inter molecular de ese medio?
Fórmula matemática: ¿Única garantía de veracidad de la hipótesis?
Una novela de ficción por absurda que sea puede cumplir a plenitud con todas las reglas gramaticales, así también podría darse el caso que una correcta fórmula matemática se utilice para fundamentar una falacia, una impostura o una errónea interpretación. En efecto, el acatamiento gramatical en un texto no es garantía de que, lo que se asevera en una novela, sea verdad; como tampoco es una prueba absoluta que, la existencia de una fórmula matemática, sea una garantía irrefutable de que la teoría sea correcta; y por lo mismo ella represente la realidad. En palabras de Mario Bunge: «A un mismo esqueleto matemático pueden asignársele una pluralidad de significados; y algunas de las estructuras matemáticas interpretadas serán verdaderas mientras que otras resultarán falsas.»
La mayor parte de las hipótesis científicas están revestidas de una correcta forma matemática, no obstante, algunas de esas hipótesis pueden resultar ser falsas.
El test de Fizeau del año 1851
El test de Fizeau, realizado en el año 1851, tuvo por el objetivo diferenciar entre la teoría del éter estático y la del éter arrastrado por el medio en que viaja la luz. Si el agua en movimiento no arrastraba al éter en absoluto no debería haber diferencia entre la velocidad de la luz en el agua en reposo. Si el agua arrastraba totalmente al éter la velocidad medida debería ser mayor. El resultado que obtuvo Fizeau - mediante su interferometría - fue sorprendente. El instrumento entregó un resultado que se interpretó que concordaba, más o menos, en un 56,5% con una de las teorías y en un 43,5% con la otra. Ver más detalles del experimento
Otros experimentos en busca del éter
El experimento Trouton-Noble fue otro famoso experimento llevado a cabo en 1901-1903 en el que se intentaba medir la velocidad de desplazamiento de la Tierra con respecto al éter por medio de efectos electrostáticos en condensadores. Sus resultados fueron también negativos confirmando los resultados de Michelson y Morley.
Referencias
- A. A. Michelson and E.W. Morley, Philos. Mag. S.5, 24 (151), 449-463 (1887)
- Análisis de la analogía usada por Michelson y Morley
- A. A. Michelson et al., Conferencia sobre el experimento Michelson-Morley, Astrophysical Journal 68, 341 (1928)
- Robert S. Shankland et al., Nuevo análisis de las observaciones del interferómetro de Dayton C. Miller, Reviews of Modern Physics, 27(2):167-178, (1955)
- Crítica al experimento
Véase también
Enlaces externos
Categorías: Experimentos físicos | Luz | Relatividad especial | 1887 -
Wikimedia foundation. 2010.