- Extensión transcendente
-
Extensión transcendente
En Teoría de Cuerpos (una rama del Álgebra), una extensión de cuerpos L:K es transcendente (también se acepta escrito como trascendente) si existe algún elemento
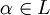 que es trascendente sobre K.
que es trascendente sobre K.El grado de una extensión trascendente es siempre infinito, pero no toda extensión de grado infinito es trascendente.
Categoría: Teoría de cuerpos
Wikimedia foundation. 2010.
