Extensión de cuerpo

Extensión de cuerpo: Extensión de cuerpo

Saltar a navegación, búsqueda

En Álgebra, las extensiones de cuerpo son el problema fundamental de la Teoría de Cuerpos. Un cuerpo es un conjunto en el que las operaciones suma y producto están definidas y "funcionan bien". Cuando se construye una extensión de un cuerpo, se busca un conjunto más grande en el que las operaciones suma y producto sigan funcionando bien y además se puedan resolver las ecuaciones polinómicas.

Contenido

1 Definición.

2 Extensión sobre un cuerpo como espacio vectorial sobre el cuerpo.

3 Extensión simple.

4 Extensiones algebraicas y trascendentes.

4.1 Teorema de Kronecker.

4.2 Homomorfismo evaluación.

4.3 Extensión algebraica.

4.3.1 Elementos algebraicos.

4.3.1.1 Polinomio mónico irreducible.

4.4 Extensión trascendente.

4.4.1 Elementos trascendentes.

5 Grado de una extensión

Definición.

Sea (K, +, ·) un cuerpo. Un cuerpo L es una extensión de K si K es un subcuerpo de L, es decir si (L,+,·) es un cuerpo y (K,+,·) es un cuerpo con la restricción a K de las operaciones + y · en L. Si L es extensión sobre K se denota L:K o L/K...

Extensión sobre un cuerpo como espacio vectorial sobre el cuerpo.

Si L es una extensión de K, entonces L es un espacio vectorial sobre K.

En efecto, La adición de K sirve también de adición en el espacio vectorial, y la multiplicación de un elemento de K por uno de L define el producto escalar del espacio vectorial:

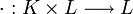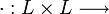Por definición de cuerpo, $(L, + )$ es grupo abeliano, y podemos considerar el producto por escalares $\cdot: K \times L \longrightarrow L$ como una restricción a $K \times L$ del producto en $\cdot: L \times L \longrightarrow$ . De esta forma es inmediato que se cumple que:

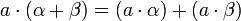$a \cdot (\alpha + \beta)= (a \cdot \alpha) + (a \cdot \beta)$ ,

$(a+b) \cdot \alpha = (a \cdot \alpha) + (b \cdot \alpha)$ ,

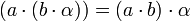$(a \cdot (b \cdot \alpha))= (a \cdot b) \cdot \alpha$ ,

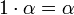$1 \cdot \alpha = \alpha$ ,

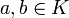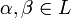cualesquiera que sean $a,b \in K$ y $\alpha,\beta \in L$ . Las dos primeras propiedades son debidas a la distributividad del producto respecto de la suma en $L$ y a que 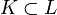$K \subset L$ , la tercera se debe a que el producto es asociativo en $L$ , y la cuarta se debe a que $K$ es subcuerpo de $L$ , por lo que el elemento unidad de $L$ es el elemento unidad de $K$ .

Extensión simple.

Artículo principal: Extensión simple

El conjunto $K(\alpha):= \{\frac{f(\alpha)}{g(\alpha)}: f,g \in K[x]\}$ . Este conjunto es un cuerpo, es extensión de $K$ , es subcuerpo de $L$ , y de hecho es la menor extensión de $K$ que contiene a $α$ . Se le denomina extensión generada por α sobre $K$ .

Extensiones algebraicas y trascendentes.

Teorema de Kronecker.

Sea $K$ un cuerpo y $p \in K[x]$ un polinomio irreducible, entonces existe alguna extensión $L : K$ de manera que $p$ tiene alguna raíz en $L$ .

Homomorfismo evaluación.

La aplicación $\beta: K[x] \longrightarrow K(\alpha)$ que a cada polinomio $p(x) \in K[x]$ le hace corresponder su evaluación en $α$ , i.e., $β(p) = p (α)$ . Esta aplicación es de hecho un isomorfismo de anillos conmutativos y unitarios, y se denomina homomorfismo evaluación.

Extensión algebraica.

Artículo principal: Extensión algebraica

Una extensión $L : K$ se dice que es algebraica si todo elemento 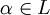$\alpha \in L$ es algebraico sobre $K$ .

Elementos algebraicos.

Artículo principal: Elemento algebraico

Supongamos que existe algún polinomio $p \in K[x]$ que tiene a $α$ por raíz.

En esta situación ( $Ker(\beta) \neq \{0\}$ , o equivalentemente, existe algún $p \in K[x]$ irreducible con $\frac{K[x]}{(p)} \cong K(\alpha)$ ) se dice que $α$ es algebraico sobre $K$ .

Un elemento es entonces algebraico sobre un cuerpo si y sólo si es raíz de algún polinomio a coeficientes en dicho cuerpo.

Polinomio mónico irreducible.

Si $α$ es un elemento algebraico sobre el cuerpo $K$ de manera que 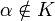$\alpha \notin K$ , el polinomio $p$ que genera al núcleo de la aplicación evaluación (i.e., $K e r β = (p)$ ) es irreducible. Dividiendo $p$ por su coeficiente principal (aquél escalar que multiplica a la mayor potencia de la variable $x$ ) se obtiene un polinomio mónico (es decir, de manera que su coeficiente principal es la unidad), que se denota por 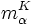$m_{\alpha}^K$ y se denomina polinomio mónico irreducible de $α$ respecto de $K$ .

Claramente, $K(\alpha) \cong \frac{K[x]}{(m_{\alpha}^K)}$ .

Extensión trascendente.

Artículo principal: Extensión transcendente

Una extensión $L : K$ se dice que es trascendente si existe algún elemento 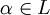$\alpha \in L$ que sea trascendente sobre $K$ .

Elementos trascendentes.

Artículo principal: Elemento trascendente

Si el Ker $(β) = {0}$ , será $β$ un monomorfismo. En ese caso, $K (x)$ es isomorfo a $K (α)$ .

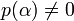Se dirá que el elemento $α$ es trascendente sobre $K$ y que $K (α)$ es una extensión trascendente sobre $K$ . Además, no existirá ningún polinomio con coeficientes en $K$ que tenga por raíz a $α$ (es decir, si $p \in K[x]$ , entonces $p(\alpha) \neq 0$ ).

Grado de una extensión

Artículo principal: Grado de una extensión

Como todo espacio vectorial tiene base, podemos calcular la dimensión de $L$ como espacio vectorial sobre $K$ , denotado por $d i m K (L)$ . Se denomina grado de la extensión $L : K$ a la dimensión de $L$ como $K$ -espacio vectorial: $[L : K] = d i m K (L)$ .

Tomemos varios ejemplos:

K = Q el cuerpo de los racionales y L = R el de los reales; Las raíces de los enteros primos (√2, √3, √5, √7,...) son linealmente independientes sobre Q, lo que implica que R visto como espacio vectorial sobre Q, es de dimensión infinita.
Otro modo de obtener este resultado es considerar los números e, e²,e³... donde el número e es la base de los logaritmos neperianos. Como e es trascendental, no existe ningún polinomio no nulo P tal que P(e) = 0, lo que significa que 1,e, e², e³ ... son linealmente independientes. De aquí la dimensión infinita.

El resultado no sorprende si se considera los cardinales de ambos conjuntos: Si la dimensión de R sobre Q fuese finita, R sería isomorfo a Qⁿ, lo que no es posible porque el cardenal de Qⁿ es el mismo que él de Q (igual al de N, aleph₀) que es estrictamente inferior al de R.

K = Q, el cuerpo de los racionales y L = Q(√2), el menor cuerpo que contiene a la vez Q y √2. L es también el conjunto de los P(√2), donde P es cualquier polinomio con coeficientes en Q.
Reagrupando los monomios de potencias pares por una parte, e impares por otra, de P(√2), se ve que los elementos de Q(√2) son los números de la forma a+b√2, con a y b racionales. Por lo tanto (1, √2) es una base de L visto como espacio vectorial sobre K, lo que significa que su dimensión es 2.
Hay que relacionar esta dimensión al hecho que √2 es raíz de un polinomio de segundo grado.

Se puede generalizar:

Si α es una raíz de un polinomio irreductible (sobre Q) de grado n, entonces Q(α) es una extensión de dimensión n sobre Q.

Obtenido de "Extensi%C3%B3n de cuerpo"

Categoría: Teoría de cuerpos

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

Extensión de cuerpo — En Álgebra, las extensiones de cuerpo son el problema fundamental de la Teoría de Cuerpos. Un cuerpo es un conjunto en el que las operaciones suma y producto están definidas y funcionan bien . Cuando se construye una extensión de un cuerpo, se… … Enciclopedia Universal
Extensión algebraica — Saltar a navegación, búsqueda En álgebra abstracta, una extensión de cuerpo L/K se dice algebraica si cada elemento de L es algebraico sobre K, i.e. si cada elemento de L es una raíz de algún polinomio distinto de cero con coeficientes en K. Las… … Wikipedia Español
Extensión de Galois — Saltar a navegación, búsqueda En álgebra abstracta, una extensión de cuerpo algebraica E/K se dice extensión de Galois (o extensión galoisiana) si es una extensión normal y separable. En este caso, se puede considerar el grupo de Galois de la… … Wikipedia Español
Extensión normal — Saltar a navegación, búsqueda En álgebra abstracta, una extensión de cuerpo algebraica N/K es normal si verifica alguna de las siguientes condiciones equivalentes: Para todo elemento , el polinomio irreducible de α en K sobre la variable x,… … Wikipedia Español
Extensión — ► sustantivo femenino 1 Acción y resultado de extender o extenderse. 2 GEOMETRÍA Propiedad que tienen los cuerpos de ocupar una parte de espacio. 3 Espacio que ocupa una cosa considerada sólo en dos dimensiones: ■ han comprado una finca de gran… … Enciclopedia Universal
Extensión algebraica — En álgebra abstracta, una extensión de cuerpo L/K se dice algebraica si cada elemento de L es algebraico sobre K, i.e. si cada elemento de L es una … Enciclopedia Universal
Extensión simple — Saltar a navegación, búsqueda En la teoría de cuerpos (una rama del álgebra), una extensión simple es una extensión de cuerpos L:K de manera que L está generado por un solo elemento. Contenido 1 Construcción 2 Definición de extensión simple … Wikipedia Español
Extensión separable — Saltar a navegación, búsqueda En matemáticas, una extensión separable de un cuerpo K es un cuerpo L que contiene a K y que puede ser generado adjuntando a K un conjunto de elementos α, tales que son raíces de polinomios separables sobre K. En… … Wikipedia Español
cuerpo — (Del lat. corpus). 1. m. Aquello que tiene extensión limitada, perceptible por los sentidos. 2. Conjunto de los sistemas orgánicos que constituyen un ser vivo. 3. Tronco del cuerpo, a diferencia de la cabeza y las extremidades. 4. Talle y… … Diccionario de la lengua española
Cuerpo (matemática) — Saltar a navegación, búsqueda Para otros usos de este término, véase Cuerpo. Un cuerpo o campo es un anillo de división conmutativo, es decir, un anillo conmutativo en el que todo elemento distinto de cero (todo elemento no nulo) es invertible… … Wikipedia Español

Marcar y compartir
Buscar en todos diccionarios
Traducir
Buscar en la internet

Compartir el artículo y extractos