Grado de una extensión

Grado de una extensión: Grado de una extensión

Saltar a navegación, búsqueda

Contenido

1 Extensión de un cuerpo como espacio vectorial sobre el cuerpo.

2 Definición del grado de una extensión.

3 Teorema de transitividad del grado.

4 Extensiones algebraicas y trascendentes.

Extensión de un cuerpo como espacio vectorial sobre el cuerpo.

Dada una extensión de cuerpos $L : K$ , podemos pensar en $L$ como en un espacio vectorial sobre el cuerpo $K$ : en efecto, por definición de cuerpo, $(L, + )$ es grupo abeliano, y podemos considerar el producto por escalares 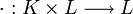$\cdot: K \times L \longrightarrow L$ como una restricción a 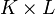$K \times L$ del producto en 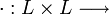$\cdot: L \times L \longrightarrow$ . De esta forma es inmediato que se cumple que:

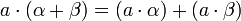$a \cdot (\alpha + \beta)= (a \cdot \alpha) + (a \cdot \beta)$ ,

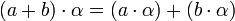$(a+b) \cdot \alpha = (a \cdot \alpha) + (b \cdot \alpha)$ ,

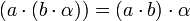$(a \cdot (b \cdot \alpha))= (a \cdot b) \cdot \alpha$ ,

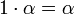$1 \cdot \alpha = \alpha$ ,

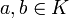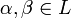cualesquiera que sean $a,b \in K$ y $\alpha,\beta \in L$ . Las dos primeras propiedades son debidas a la distributividad del producto respecto de la suma en $L$ y a que 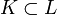$K \subset L$ , la tercera se debe a que el producto es asociativo en $L$ , y la cuarta se debe a que $K$ es subcuerpo de $L$ , por lo que el elemento unidad de $L$ es el elemento unidad de $K$ .

Definición del grado de una extensión.

Como todo espacio vectorial tiene base, podemos calcular la dimensión de $L$ como espacio vectorial sobre $K$ , denotado por $d i m K (L)$ . Se denomina grado de la extensión $L : K$ a la dimensión de $L$ como $K$ -espacio vectorial: $[L : K] = d i m K (L)$ .

Teorema de transitividad del grado.

Sea $L$ una extensión de $K$ , y sea $E$ un subcuerpo de $L$ que es a su vez extensión de $K$ . Entonces se cumple que $[L : K] = [L : E][E : K]$ .

Demostración:

Sea 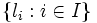$\{l_i: i \in I\}$ una base del $E$ -espacio vectorial $L$ (es decir, consideramos $L$ como un espacio vectorial sobre el cuerpo $E$ , y obtenemos una base) y 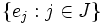$\{e_j:j \in J\}$ una base del $K$ -espacio vectorial $E$ . Sea 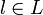$l \in L$ un elemento arbitrario. Existirá una única combinación lineal (que será finita, nosotros consideramos aquí que los coeficientes de la combinación lineal son eventualmente nulos) de tal manera que 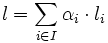$l=\sum_{i \in I}\alpha_i \cdot l_i$ , siendo cada 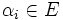$\alpha_i \in E$ . 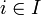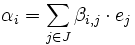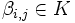De la misma forma, existirá una única combinación lineal (cuyos coeficientes serán eventualmente nulos) de tal manera que tenemos que para cada $i \in I$ es $\alpha_i=\sum_{j \in J}\beta_{i,j} \cdot e_j$ , siendo cada $\beta_{i,j} \in K$ .

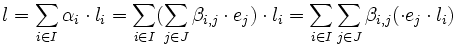$l=\sum_{i \in I}\alpha_i \cdot l_i = \sum_{i \in I}(\sum_{j \in J}\beta_{i,j} \cdot e_j) \cdot l_i= \sum_{i \in I}\sum_{j \in J}\beta_{i,j} (\cdot e_j \cdot l_i)$ .

Esto demuestra que 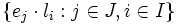$\{e_j \cdot l_i: j \in J, i \in I\}$ es un sistema generador del $K$ -espacio vectorial $L$ .

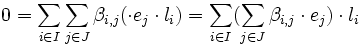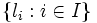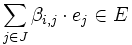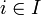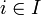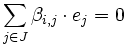Supongamos ahora que tenemos una combinación lineal $0=\sum_{i \in I}\sum_{j \in J}\beta_{i,j} (\cdot e_j \cdot l_i)= \sum_{i \in I}(\sum_{j \in J}\beta_{i,j} \cdot e_j) \cdot l_i$ . Como $\{l_i: i \in I\}$ es base del $E$ -espacio vectorial $L$ y $\sum_{j \in J}\beta_{i,j} \cdot e_j \in E$ cualquiera que sea el $i \in I$ , tenemos que ha de ocurrir que en cada $i \in I$ sea $\sum_{j \in J}\beta_{i,j} \cdot e_j=0$ . Ahora bien, como 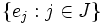$\{e_j:j \in J\}$ es base del $K$ -espacio vectorial $E$ , entonces ha de ser $b i, j = 0$ , cualesquiera que sean el 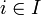$i \in I$ y el $j \in J$ . 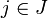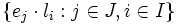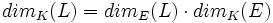Así pues, $\{e_j \cdot l_i: j \in J, i \in I\}$ es una familia libre del $K$ -espacio vectorial $L$ , con lo cual es una base de $L$ como K-espacio vectorial, y su cardinal es $dim_K(L)=dim_E(L) \cdot dim_K(E)$ .

Extensiones algebraicas y trascendentes.

El grado de una extensión resulta muy útil para determinar si una extensión es algrebraica o trascendente.

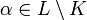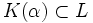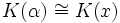Si una extensión L:K es trascendente, existirá al menos un $\alpha \in L \setminus K$ de manera que $α$ sea un elemento trascendente sobre $K$ . Así pues, $K(\alpha) \subset L$ , luego $[L:K]=dim_K(L)\geq dim_K(K(\alpha))$ . Pero como $K(\alpha) \cong K(x)$ (por ser $α$ trascendente sobre $K$ ), y por otro lado $K[x] \subset K(x)$ (con lo que $dim_K(K[x]) \leq dim_K(K(x))$ ) y $dim_K(K[x])= \infty$ , resulta que $[L:K]=dim_K(L)\geq dim_K(K(\alpha))=dim_K(K(x)) \geq dim_K(K[x])) = \infty$ .

Concluimos que toda extensión trascendente tiene grado infinito, y que toda extensión de grado finito es algebraica. Ahora bien, puede ocurrir que una extensión de grado infinito sea algebraica.

Si $[L : K] = 1$ , será entonces $L = K$ . Si tomamos un elemento 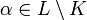$\alpha \in L\setminus K$ que sea algebraico sobre $K$ , entronces existirá un polinomio mónico irreducible 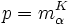$p=m_{\alpha}^K$ de manera que $K(\alpha) \cong \frac{K[x]}{(p)}$ . Si $d e g (p) = n$ , entonces ${1 + (p), x + (p),..., x n - 1 + (p)}$ es una base de $\frac{K[x]}{(p)}$ , con lo cual $[K(\alpha):K]= dim_K(K(\alpha))= dim_K(\frac{K[x]}{(p)})= n =deg(p)=deg(m_{\alpha}^K)$ .

Obtenido de "Grado de una extensi%C3%B3n"

Categoría: Teoría de cuerpos

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

Grado de una extensión — Extensión de un cuerpo como espacio vectorial sobre el cuerpo. Dada una extensión de cuerpos , podemos pensar en como en un espacio vectorial sobre el cuerpo : en efecto, por definición de cuerpo, es grupo abeliano, y podemos considerar el… … Enciclopedia Universal
Extensión de cuerpo — Saltar a navegación, búsqueda En Álgebra, las extensiones de cuerpo son el problema fundamental de la Teoría de Cuerpos. Un cuerpo es un conjunto en el que las operaciones suma y producto están definidas y funcionan bien . Cuando se construye una … Wikipedia Español
Grado — puede referirse a: el grado de comparación o significación de un adjetivo; el grado como distinción académica en educación; el grado en matemática, además de nombrar a distintas unidades de medida de ángulos nombra: el grado de un polinomio, y… … Wikipedia Español
Extensión transcendente — Saltar a navegación, búsqueda En Teoría de Cuerpos (una rama del Álgebra), una extensión de cuerpos L:K es transcendente (también se acepta escrito como trascendente) si existe algún elemento que es trascendente sobre K. El grado de una extensión … Wikipedia Español
Grado de extensión de un cuerpo — Contenido 1 Extensión de un cuerpo como espacio vectorial sobre el cuerpo. 2 Definición del grado de una extensión. 3 Teorema de transitividad del grado … Wikipedia Español
Grado (matemática) — Este ártículo trata del grado tal y como es empleado en el área de las matemáticas. Para significados alternativos de esta palabra, véase grado. En matemáticas existen diferentes significados de la palabra grado dependiendo del área matemática de … Wikipedia Español
Grado — I (Del lat. gradus, graduación.) ► sustantivo masculino 1 Situación, valor, calidad o medida de una cosa: ■ todavía no sabemos cuál es el grado de complejidad de este asunto. SINÓNIMO nivel 2 Cada una de las partes de la escalera en la que se… … Enciclopedia Universal
Extensión transcendente — En Teoría de Cuerpos (una rama del Álgebra), una extensión de cuerpos es transcendente (también se acepta escrito como trascendente) si existe algún elemento que es trascendente sobre . El grado de una extensión trascendente es siempre infinito,… … Enciclopedia Universal
Extensión simple — Saltar a navegación, búsqueda En la teoría de cuerpos (una rama del álgebra), una extensión simple es una extensión de cuerpos L:K de manera que L está generado por un solo elemento. Contenido 1 Construcción 2 Definición de extensión simple … Wikipedia Español
Extensión algebraica — Saltar a navegación, búsqueda En álgebra abstracta, una extensión de cuerpo L/K se dice algebraica si cada elemento de L es algebraico sobre K, i.e. si cada elemento de L es una raíz de algún polinomio distinto de cero con coeficientes en K. Las… … Wikipedia Español

Marcar y compartir
Buscar en todos diccionarios
Traducir
Buscar en la internet

Compartir el artículo y extractos