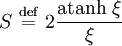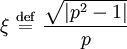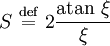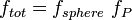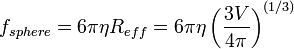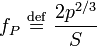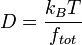Factores de fricción de Perrin

Factores de fricción de Perrin

Factores de fricción de Perrin

En hidrodinámica, los factores de fricción de Perrin son factores de ajuste de tipo multiplicativo a la fricción traslacional y rotacional de un esferoide rígido, con respecto a los factores de fricción correspondientes a esferas del mismo volumen. Estos factores fueron calculado por primera vez por Jean-Baptiste Perrin.

Estos factores son aplicables a esferoides (por ejemplo, elipsoides de revolución), que quedan caracterizados por una relación axial p = (a/b), definida entre el semieje axial a (o sea el semieje a lo largo del eje de revolución) dividido por el semieje ecuatorial b. En esferoides prolados, la relación axial es p > 1 dado que el semieje axial es más largo que los semiejes ecuatoriales. En forma análoga, en esferoides oblatos, la relación axial es p < 1 dado que el semieje axial es más corto que los semiejes ecuatoriales. Finalmente, para una esfera, la relación axial es p = 1, dado que los tres semiejes son de igual longitud.


Factor S de Perrin

En las ecuaciones que se presentan a continuación, se define el factor S de Perrin. Para esferoides prolatos (es decir esferoides con forma de cigarro con dos ejes cortos y un eje largo)

S \ \stackrel{\mathrm{def}}{=}\ 2 \frac{\mathrm{atanh} \ \xi}{\xi}

donde el parámetro ξ se define por la expresión

\xi \ \stackrel{\mathrm{def}}{=}\ \frac{\sqrt{\left| p^{2} - 1 \right|}}{p}

En forma similar, para esferoides oblatos (o sea esferoides con forma de disco con dos ejes largos y un eje corto)

S \ \stackrel{\mathrm{def}}{=}\ 2 \frac{\mathrm{atan} \ \xi}{\xi}

Para esferas, S = 2, lo que se puede demostrar si se toma el límite para 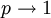p \rightarrow 1 en las expresiones de esferoides prolados u oblatos.


Factor de fricción de traslación

El coeficiente de fricción de un esferoide arbitrario de volumen V es:

f_{tot} = f_{sphere} \ f_{P}

donde fsphere es el coeficiente de fricción traslacional de una esfera de volumen equivalente (ley de Stokes)

f_{sphere} = 6 \pi \eta R_{eff} = 6\pi \eta \left(\frac{3V}{4\pi}\right)^{(1/3)}

y fP es el factor de fricción de traslación de Perrin

f_{P} \ \stackrel{\mathrm{def}}{=}\ \frac{2p^{2/3}}{S}

El coeficiente de fricción está relacionado con la constante de difusión D mediante la relación de Einstein

D = \frac{k_{B}T}{f_{tot}}

por lo tanto se puede medir directamente, ftot utilizando ultracentrifugación analítica, o indirectamente utilizando alguno de los varios métodos que están disponibles para medir la constante de difusión (por ejemplo, NMR y dispersión dinámica de luz).

Referencias

  • Cantor CR and Schimmel PR. (1980) Biophysical Chemistry. Part II. Techniques for the study of biological structure and function, W. H. Freeman, p. 561-562.
  • Koenig SH. (1975) "Brownian Motion of an Ellipsoid. A Correction to Perrin's Results." Biopolymers 14: 2421-2423.
Obtenido de "Factores de fricci%C3%B3n de Perrin"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Anisotropía fluorescente — Saltar a navegación, búsqueda En química, la anisotropía fluorescente mide la difusión rotacional de una molécula a partir de la diferencia en la correlacíon (decorrelación) de polarización en fluorescencia, es decir entre los fotones que excitan …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”