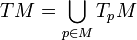Fibrado tangente

Fibrado tangente

Fibrado tangente

En matemáticas, el fibrado tangente de una variedad es la unión de todos los espacios tangentes en cada punto de la variedad.

Definición como direcciones de las curvas

Supongamos que M es una variedad Ck, y φ: U → Rn donde U es un subconjunto abierto de M, y n es la dimensión de la variedad, en la carta φ(.) además suponga que TpM es el espacio tangente en un punto p de M. Entonces el fibrado tangente,

{TM} = \bigcup_{p \in M} T_{p}M

Es útil, para distinguir entre el fibrado y el espacio tangente, considerar sus dimensiones, 2n, n respectivamente. Es decir, el fibrado tangente considera dimensiones tanto de las posiciones en la variedad así como de las direcciones tangentes.

Puesto que podemos definir un función de la proyección, π para cada elemento del fibrado tangente que da el elemento en la variedad cuyo espacio tangente contiene el primer elemento, todo fibrado tangente es también un fibrado.

Obtenido de "Fibrado tangente"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Fibrado tangente — En matemáticas, el fibrado tangente de una variedad es la unión de todos los espacios tangente en cada punto de la variedad …   Enciclopedia Universal

  • Fibrado vectorial — Saltar a navegación, búsqueda En matemáticas, un fibrado vectorial es una construcción geométrica donde a cada punto de un espacio topológico (o variedad, o variedad algebraica) unimos un espacio vectorial de una manera compatible, de modo que… …   Wikipedia Español

  • Fibrado cotangente — Saltar a navegación, búsqueda En geometría diferencial, el fibrado cotangente de una variedad es la unión de todos los espacios cotangente en cada punto de la variedad. Contenido 1 Uno formas 2 El fibrado cotangente como espacio de fase …   Wikipedia Español

  • Fibrado asociado — Saltar a navegación, búsqueda En matemáticas, la teoría de los fibrados con un grupo de estructura G (un grupo topológico) permite una operación de creación de un fibrado asociado, en el cual la fibra típica de un fibrado cambia de F1 a F2, que… …   Wikipedia Español

  • Fibrado vectorial — En matemáticas, un fibrado vectorial es una construcción geométrica donde a cada punto de un espacio topológico (o variedad, o variedad algebraica) unimos un espacio vectorial de una manera compatible, de modo que todos esos espacios vectoriales …   Enciclopedia Universal

  • Fibrado principal — Saltar a navegación, búsqueda En matemática, un G fibrado principal es una clase especial de fibrado para la cual las fibras son todas espacios homogéneos principales respecto a un grupo topológico. Los G fibrados principales son G fibrados en el …   Wikipedia Español

  • Espacio tangente — Saltar a navegación, búsqueda El plano que toca a la esfera en un solo punto es llamado plano tangente. Cada punto de la esfera tiene asociado un plano tangente. Para la esfera los puntos antipodales tiene planos tangente paralelos En geometría… …   Wikipedia Español

  • Conexión de Cartan — En matemática, la construcción de la conexión de Cartan en geometría diferencial es una generalización amplia del concepto de la conexión, basado en una comprensión del papel del grupo afín en el acercamiento usual. Fue desarrollado por Élie… …   Wikipedia Español

  • Variedad de Riemann — Ejemplo de variedad de Riemann bidimensional con un sistema de coordenadas ortogonales definido sobre ella, y varias subvariedades curvas de la misma. En la geometría de Riemann, una variedad de Riemann es una variedad diferenciable real en la… …   Wikipedia Español

  • Espacio de configuración — Saltar a navegación, búsqueda En mecánica clásica y mecánica lagrangiana, el espacio de configuración es el espacio de todas las posibles posiciones instantáneas de un sistema mecánico. El espacio de configuración de un sistema mecánico tiene… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”