En matemática, y específicamente en teoría del orden, retículos y topología, un filtro es un subconjunto especial de un conjunto parcialmente ordenado. Un caso especial utilizado con frecuencia es cuando el conjunto ordenado considerado el conjunto potencia de un conjunto S (es decir, el conjunto conformado por todos los subconjuntos de S), ordenado mediante la relación de inclusión. La noción de dual de un filtro es la de ideal.

Los filtros fueron introducidos por Henri Cartan in 1937^{[1] [2]} y utilizados subsecuentemente por Bourbaki en su libro Topologie Générale como una alternativa a la noción similar de red desarrollada en 1922 por E. H. Moore y H. L. Smith.

Contenido 1 Definición general 2 Filtros de conjuntos 2.1 Ejemplos 3 Notes 4 References

Definición general

Un subconjunto no vacío F de un conjunto parcialmente ordenado (P,≤) es un filtro si se dan las siguientes condiciones:

1. Para cada x en F, x ≤ y implica que y también está en F. ('F es un conjunto "upper"', "hacia arriba")
2. Para cada x, y en F, existe cierto elemento z en F, tal que z ≤ x y z ≤ y. (F es un conjunto filtrado)

Un filtro se dice propio si no es igual a todo el conjunto P completo.

Mientras que la definición de arriba es la manera más general para definir un filtro sobre "posets" arbitrarios, originalmente se definió sólo para los reticulados, en cuyo caso, la definición de arriba puede caracterizarse por la siguiente proposición equivalente:

Un subconjunto no vacío F de un reticulado (P,≤) es un filtro, si y sólo si es un conjunto "upper" que es cerrado bajo finitas "meets": 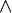(ínfimo), esto es, para todo x e y en F, se tiene que 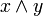está también en F.

El filtro más pequeño que contenga cierto elemento dado p es un filtro principal y p es un elemento principal en esta situación. El filtro principal para p viene dado por el conjunto {x en P | p ≤ x} y se denota poniendo delante de la p una flecha hacia arriba.

La noción dual de la de filtro, esto es, el concepto que se obtiene "dando la vuelta" a todas las " ≤ " y cambiando 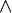por 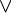, es el de ideal. Debido a esta dualidad la discusión sobre los filtros repite la de los ideales. De ahí que la mayor parte de la información adicional sobre ellos (incluyendo la de filtros maximales y filtros primos) se encuentra en el artículo sobre ideales. Existe también un artículo separado sobre ultrafiltros.

Filtros de conjuntos

Un caso importante de filtros en teoría del orden son los filtros de conjuntos, que se obtienen tomando el conjunto potencia de un conjunto dado S, visto como orden parcial y ordenado por la inclusión de subconjuntos. Con ello tendremos que un filtro F sobre un conjunto S es un conjunto de subconjuntos de S con las siguientes propiedades:

1. S está en F. (F es no vacío)
2. F no contiene al conjunto vacío. (F es propio)
3. Si A y B están en F, también su intersección. ("F es cerrado bajo intersecciones finitas ")
4. Si A está en F y A es un subconjunto de B, entonces B está en F, para todos los subconjuntos B de S. (" F es cerrado bajo supercontenencias ")

Las tres primeras propiedades implican que un filtro de conjunto tiene la Propiedad de la Intersección Finita. Nótese que con esta definición, un filtro de conjunto es en efecto un filtro; de hecho es un filtro propio. Debido a ello, algunas veces es llamado filtro propio de un conjunto; desde luego, tan claro como sea el contexto del conjunto, el nombre más breve es suficiente.

Una base de filtro es un subconjunto B de P(S) con las siguientes propiedades:

1. La intersección de cualquier par de conjuntos de B, contiene un conjunto de B.
2. B es no vacío y el conjunto vacío no está en B.

Dado una base de filtro B, se puede obtener un filtro (propio) al incluir todos los conjuntos de P(S) que contienen a algún subconjunto de B. El filtro que resulta se dice generado por la base de filtro B. Todo filtro es a fortiori una base de filtro, de modo que el proceso de pasar de una base de filtro a un filtro puede ser visto como una especie de completación.

Si B y C son dos bases de filtro en S, se dice que C es más fino que B (o que C es un refinamiento de B), si para cada B₀ ∈ B existe C₀ ∈ C tal que C₀ ⊆ B₀.

Para las bases de filtros B y C, si B es más fina que C, y C es más fina que B, entonces se dice que B y C son bases de filtro equivalentes. Dos bases de filtro son equivalentes si y sólo si los filtros que generan son iguales.

Para las bases de filtros A, B y C, si A es más fina que B, y B es más fina que C, A es más fina que C. Por tanto la relación de refinamiento es un preorden en el conjunto de las bases de filtros, y el pasaje de una base de filtro a un filtro es un ejemplo de un preordenamiento al ordenamiento parcial asociado.

Dado un subconjunto T de P(S) podemos preguntar cuándo existe un filtro más pequeño F que contiene a T. Tal filtro existe si y sólo si la intersección finita de subconjuntos de T es no vacía. Llamamos a T subbase de F, y decimos que F está generado por T. La subbase T puede construirse tomando todas las intersecciones finitas de T, el cual es entonces una base de filtro para F.

Ejemplos

• Sea S un conjunto no vacio y C un subconjunto de S no vacio. Entonces {C} es una base de filtro. El filtro que genera (es decir la coleccion de todos los subconjuntos que contienen a C) es llamado filtro principal generado por C.

• Un filtro se dice que es filtro libre si la interseccion de todos sun elementos es vacía. Un filtro principal no es

libre. Ya que la interseccion de cualquier numero finito de miembros de un filtro es además un miembro, ningún filtro sobre un conjunto finito es libre, y de hecho es el filtro principal generado por la interseccion común de todos sus miembros. Un filtro no principal sobre un conjunto infinito no es libre necesariamente.

• El filtro de Fréchet de un conjunto infinito S es el conjunto de todos los subconjuntos de S que tienen complemento finito. El filtro de Frechet es libre, y está contenido en todo filtro libre sobre S.

• Una estructura uniforme sobre un conjunto X es (en particular) un filtro en XxX.

• Un filtro en un conjunto parcialmente ordenado puede construirse usando el Lema de Rasiowa-Sikorski. casi siempre usado en forzamiento.

Notes

References

• Nicolas Bourbaki, General Topology (Topologie Générale), ISBN 0-387-19374-X (Ch. 1-4): Provides a good reference for filters in general topology (Chapter I) and for Cauchy filters in uniform spaces (Chapter II)
• Stephen Willard, General Topology, (1970) Addison-Wesley Publishing Company, Reading Massachusetts. (Provides an introductory review of filters in topology.)
• David MacIver, Filters in Analysis and Topology (2004) (Provides an introductory review of filters in topology and in metric spaces.)
• Burris, Stanley N., and H.P. Sankappanavar, H. P., 1981. A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2.