- Retículo (orden)
-
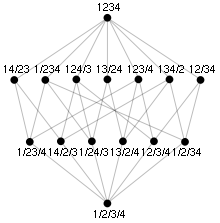 Diagrama de Hasse del retículo de particiones del conjunto {1,2,3,4}.
Diagrama de Hasse del retículo de particiones del conjunto {1,2,3,4}.
En matemática, un retículo es una determinada estructura algebraica con dos operaciones binarias, o bien un conjunto parcialmente ordenado con ciertas propiedades específicas (siendo equivalentes ambos enfoques). El término "retículo" viene de la forma de los diagramas de Hasse de tales órdenes.
Contenido
Definición como conjunto ordenado
En teoría de conjuntos, un retículo, red o lattice es un conjunto parcialmente ordenado en el cual para cada par de elementos existen un supremo y un ínfimo, esto es:
Un conjunto parcialmente ordenado (L, ≤) se denomina retículo si satisface las siguientes propiedades:
- Existencia del supremo por pares
- Para cualesquiera dos elementos a y b de L, el conjunto {a, b} tiene un supremo:
 (también conocido como mínima cota superior, o join en idioma inglés).
(también conocido como mínima cota superior, o join en idioma inglés). - Existencia del ínfimo por pares
- Para cualesquiera dos elementos a y b de L, el conjunto {a, b} tiene un ínfimo:
 (también conocido como máxima cota inferior, o meet en idioma inglés).
(también conocido como máxima cota inferior, o meet en idioma inglés).
El supremo y el ínfimo de a y b se denotan por
 y
y  , respectivamente, lo que define a
, respectivamente, lo que define a  y
y  como operaciones binarias. El primer axioma dice que L es un semiretículo superior; el segundo que L es un semiretículo inferior. Ambas operaciones son monótonas con respecto al orden: a1 ≤ a2 y b1 ≤ b2 implica que a1
como operaciones binarias. El primer axioma dice que L es un semiretículo superior; el segundo que L es un semiretículo inferior. Ambas operaciones son monótonas con respecto al orden: a1 ≤ a2 y b1 ≤ b2 implica que a1 b1 ≤ a2
b1 ≤ a2  b2 y a1
b2 y a1 b1 ≤ a2
b1 ≤ a2 b2.
b2.Se sigue por inducción matemática que para todo subconjunto finito no vacío de un retículo existen un supremo y un ínfimo.
Nótese que aún en un conjunto parcialmente ordenado (L, ≤) arbitrario, la existencia de algún supremo (o ínfimo) z para un subconjunto finito no vacío S de L implica que este supremo (o ínfimo) z es único, puesto que de existir dos o más cotas superiores (o inferiores) de S que sean incomparables entre sí, el supremo (o ínfimo) por definición no existe.
Definición algebraica
En álgebra, en sentido inverso, un retículo es un conjunto L, provisto de dos operaciones binarias
 y
y  , tales que para cualesquiera a, b, c en L se cumplen
, tales que para cualesquiera a, b, c en L se cumplena  b = b
b = b  a
aa  b = b
b = b  a
alas leyes de conmutatividad a  (b
(b  c) = (a
c) = (a  b)
b)  c
ca  (b
(b  c) = (a
c) = (a  b)
b)  c
clas leyes de asociatividad a  (a
(a  b) = a
b) = aa  (a
(a  b) = a
b) = alas leyes de absorción condiciones de las que se derivan a  a = a
a = aa  a = a
a = alas leyes de idempotencia Si las dos operaciones satisfacen estas reglas algebraicas, entonces a su vez definen un orden parcial ≤ en L por la regla siguiente: a ≤ b si y sólo si a
 b = b, o, equivalentemente, a
b = b, o, equivalentemente, a  b = a.
b = a.L, junto con el orden parcial ≤ así definido, sería entonces un retículo en el sentido antedicho de la teoría del orden.
Inversamente, si se da un retículo (L, ≤) en términos de la teoría del orden, y escribimos a
 b para el supremo de {a, b} y a
b para el supremo de {a, b} y a  b para el ínfimo de {a, b}, entonces (L,
b para el ínfimo de {a, b}, entonces (L,  ) satisface todos los axiomas de un retículo definido algebraicamente.
) satisface todos los axiomas de un retículo definido algebraicamente.Por tanto L es un semiretículo con respecto a cada operación por separado, es decir, un semigrupo conmutativo, con idempotencia de cada uno de sus elementos. Las operaciones interactúan a través de las leyes de absorción.
Al permutar las operaciones se obtiene el retículo dual de L.
Homomorfismos
La clase de todos los retículos forma una categoría si definimos un homomorfismo entre dos retículos (L,
 ) y (N,
) y (N,  ) como una función f: L
) como una función f: L  N tal que
N tal que- f(a
 b) = f(a)
b) = f(a)  f(b);
f(b); - f(a
 b) = f(a)
b) = f(a)  f(b);
f(b);
para todo a y b en L. Si es un homomorfismo biyectivo, entonces su inverso es también un homomorfismo, y se llama un isomorfismo de retículos. Los dos retículos implicados son entonces isomorfos; para todos los propósitos prácticos, son iguales y se diferencian solamente en la notación de sus elementos.
Cada homomorfismo es una función monótona entre los dos retículos, pero no cada función monótona da un homomorfismo de retículo: además necesitamos la compatibilidad con supremos e ínfimos finitos.
Retículos particulares
En lo que sigue, por "retículo L" siempre nos referiremos a (L,
 ,
,  ).
).Un retículo L se denomina distributivo, si sus operaciones son doblemente distributivas:
 para todo
para todo  y
y para todo
para todo  .
.
Como estos dos juicios son equivalentes entre sí, basta exigir el cumplimiento de una de las dos leyes distributivas.
Un retículo L se denomina modular, si se cumple que:
 para todo
para todo  .
.
Para un retículo L a su vez son equivalentes:
- L es modular.
 para todo
para todo  .
. para todo
para todo  .
. para todo
para todo  .
.
Todo retículo distributivo es modular, pero el juicio inverso no se cumple. Un retículo no modular siempre contiene al retículo N5 como subretículo.
En caso de que la operación
 tenga un elemento neutro 0,
tenga un elemento neutro 0,a este se lo denomina el 'elemento cero' del retículo. Es único y es el elemento menor con respecto al orden natural del retículo:
 y
y 
El retículo se denomina entonces retículo con cota inferior.
En caso de que la operación
 tenga un elemento neutro 1,
tenga un elemento neutro 1,a este se lo denomina el 'elemento uno' del retículo. Es único y es el elemento mayor con respecto al orden natural del retículo:
 y
y
El retículo se denomina entonces retículo con cota superior.
El elemento neutral de una de las operaciones es entonces un elemento absorbente de la otra. Un retículo se denomina acotado si tiene cota superior e inferior, es decir, si ambas operaciones tienen elemento neutro.
Para un elemento dado a de un retículo acotado, al elemento b con la propiedad
 y
y
se lo denomina complemento de a. Un retículo acotado, en el que cada uno sus elementos tiene complemento, se denomina complementado.
Un retículo distributivo complementado se denomina álgebra de Boole o retículo de Boole; cuando en lugar del complemento solamente existe un así llamado pseudocomplemento relativo, se habla de una álgebra de Heyting.
Un retículo L se denomina completo si todo subconjunto (inclusive los subconjuntos vacío o posiblemente suconjuntos infinitos) tiene un supremo y un ínfimo.
Para cada subconjunto M basta exigir la existencia del supremo, ya que
Un elemento a de un retículo completo L se denomina compacto (según una propiedad similar en topología), si todo subconjunto M de L con
contiene un subconjunto finito E tal que
 .
.
Un retículo L se denomina algebraico, si es completo y si todo elemento de L es un supremo de elementos compactos.
Propiedades
Todo retículo completo L es acotado, con
 y
y
Todo retículo finito, no vacío L es completo, por lo que también es acotado.
En un retículo distributivo y acotado, el complemento de un elemento a es único si existe, lo que suele denotarse como ac (particularmente en el caso de retículos de subconjuntos) o bien ¬a (particularmente en aplicaciones de lógica).
- Demostración: Sean b y c complementos de a, queremos mostrar que b = c. Ahora se cumple que b = b
 1 = b
1 = b  (a
(a  c) = (b
c) = (b  a )
a )  (b
(b  c) = b
c) = b  c. Análogamente se muestra que c = b
c. Análogamente se muestra que c = b  c, por lo que b = c.
c, por lo que b = c.
Sin embargo, si el retículo no es distributivo, pueden existir diversos complementos; va un ejemplo más adelante.
En un retículo distributivo acotado se verifica
- ¬0 = 1, ¬1 = 0.
Si a tiene un complemento ¬a, entonces también ¬a tiene un complemento, que es:
- ¬(¬a) = a.
Para otras propiedades de los retículos booleanos véase ese artículo.
Ejemplos de retículos
- Los subconjuntos de un conjunto dado, ordenados por inclusión. El supremo está dado por la unión y el ínfimo por la intersección de subconjuntos.
- El intervalo unidad [0, 1] y la recta extendida de números reales, con el orden total familiar y los usuales supremo e ínfimo.
- Los enteros no negativos, ordenados por divisibilidad. El supremo viene dado por el mínimo común múltiplo y el ínfimo por el máximo común divisor.
- Los subgrupos de un grupo, ordenado por la inclusión. El supremo viene dado por el subgrupo generado por la unión de los grupos y el ínfimo viene dado por la intersección.
- Los submódulos de un módulo, ordenado por la inclusión. El supremo viene dado por de la suma de submódulos y el ínfimo por la intersección.
- Los ideales de un anillo, ordenado por la inclusión. El supremo viene dado por la suma de ideales y el ínfimo por la intersección.
- Los conjuntos abiertos de un espacio topológico, ordenados por la inclusión. El supremo viene dado por la unión de conjuntos abiertos y el ínfimo por el interior de la intersección.
- los subconjuntos convexos de un espacio vectorial real o complejo, ordenado por la inclusión. El ínfimo viene dado por la intersección de conjuntos convexos y el supremo por la clausura convexa de la unión.
- Las topologías en un conjunto, ordenadas por la inclusión. El ínfimo viene dado por la intersección de topologías, y el supremo por la topología generada por la unión de las topologías.
- El retículo de todas las relaciones binarias transitivas en un conjunto.
- El retículo de todas las relaciones de equivalencia en un conjunto; la relación de equivalencia ~ se considera ser más pequeño (o "más fino") que ≈ si x~y implica siempre x≈y.
El teorema de Knaster-Tarski establece que el conjunto de puntos fijos de una función monótona en un retículo completo es asimismo un retículo completo.
El retículo de submódulos de un módulo y el retículo de los subgrupos normales de un grupo tienen la propiedad especial que x
 (y
(y  (x
(x  z)) = (x
z)) = (x  y)
y)  (x
(x  z) para todo x, y y z en el retículo. Un retículo con esta propiedad se llama un retículo modular. La condición de la modularidad puede también ser establecida como sigue: Si x ≤ z entonces para todo y tenemos la identidad x
z) para todo x, y y z en el retículo. Un retículo con esta propiedad se llama un retículo modular. La condición de la modularidad puede también ser establecida como sigue: Si x ≤ z entonces para todo y tenemos la identidad x  (y
(y  z) = (x
z) = (x  y)
y)  z.
z.Un retículo se llama distributivo si
 distribuye a
distribuye a  , es decir, x
, es decir, x  (y
(y  z) = (x
z) = (x  y)
y)  (x
(x  z). equivalentemente,
z). equivalentemente,  distribuye
distribuye  . Todos los retículos distributivos son modulares. Dos tipos importantes de retículos distributivos son los conjuntos totalmente ordenados y las álgebras booleanas (como el retículo de todos los subconjuntos de un conjunto dado). El retículo de los números naturales, ordenados por divisibilidad, es también distributivo. Otras leyes comunes de distributividad (especialmente la ley de distributividad completa) se dan en el artículo sobre distributividad en teoría del orden.
. Todos los retículos distributivos son modulares. Dos tipos importantes de retículos distributivos son los conjuntos totalmente ordenados y las álgebras booleanas (como el retículo de todos los subconjuntos de un conjunto dado). El retículo de los números naturales, ordenados por divisibilidad, es también distributivo. Otras leyes comunes de distributividad (especialmente la ley de distributividad completa) se dan en el artículo sobre distributividad en teoría del orden.Nociones importantes de la teoría de retículos
En lo siguiente, sea L un retículo. Definimos algunas nociones de la teoría del orden que son de importancia particular en teoría de retículos.
Un elemento x de L se llama supremo-irreducible si y sólo si
- x = a
 b implica x = a o x = b para cualquier a, b en L,
b implica x = a o x = b para cualquier a, b en L,
- si L tiene un 0, de x se requiere a veces ser diferente de 0.
Cuando la primera condición se generaliza a supremos arbitrarios Vai, x se llama totalmente supremo-irreducible. la noción dual se llama ínfimo-irreducibilidad. A veces uno también utiliza los términos
 -irreducibles y
-irreducibles y  -irreducibles, respectivamente.
-irreducibles, respectivamente.Un elemento x de L se llama supremo-primo si y sólo si
- x ≤ a
 b implica x ≤ a o x ≤ b,
b implica x ≤ a o x ≤ b,
- Si L tiene 0, de x se requiere a veces ser diferente de 0.
Una vez más esto se puede generalizar para obtener la noción totalmente supremo-primo y dualizar para ínfimo-primo. Cualquier elemento supremo-primo es también supremo-irreducible, y cualquier elemento ínfimo-primo es también ínfimo-irreducible. Si el retículo es distributivo el inverso es también verdad.
Otras nociones importantes en teoría de retículos son ideal y su noción dual filtro. Ambos términos describen subconjuntos especiales de un retículo (o de cualquier conjunto parcialmente ordenado en general). Los detalles se pueden encontrar en los artículos respectivos.
Referencias
Bibliografía
- Garrett Birkhoff, 1967. Lattice Theory, 3rd ed. Vol. 25 of AMS Colloquium Publications. American Mathematical Society. ISBN 9780821810255
- Robert P. Dilworth y Crawley, Peter, 1973. Algebraic Theory of Lattices. Prentice-Hall. ISBN 9780130222695.
- George Grätzer, 1978. General Lattice Theory. Birkhäuser. ISBN 9783764369965.
- Hans Hermes, 1963. La Teoría de Retículos y Su Aplicación a la Lógica Matemática. Consejo Superior de Investigaciones Científicas. ISBN 9788400031039
Categoría:- Teoría de retículos
Wikimedia foundation. 2010.




