Red de flujo

Red de flujo

Red de flujo

Entendiendo una red de flujo como un grafo dirigido, donde la fuente es quien produce o inicia el traspaso de algún material o producto por los arcos, estos últimos, vistos como caminos o conductos y tomando en cuenta la ley de corrientes de Kirchoff, donde, la suma de flujos entrantes a un vértice debe ser igual a la suma de flujos saliendo del vértice.

Descripción matemática

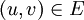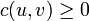Una red de flujo es un grafo dirigido G = (V,E) en donde cada arco (u,v) \in E tiene una capacidad no negativa c(u,v) \ge 0.

Se distinguen dos vértices: la fuente s y el destino t.

Se supone que cada vértice se encuentra en alguna ruta de s a t.

Un flujo en G es una función 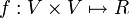f: V \times V \mapsto R tal que

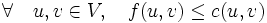
  • Restricción de capacidad: \forall \quad u,v \in V,\quad f(u,v) \le c(u,v)
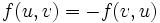
  • Simetría: f(u,v) = - f(v,u) \,
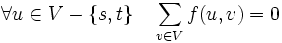
  • Conservación: \forall u \in V - \left \{ s,t \right \} \quad \sum_{v \in V} f(u,v) = 0

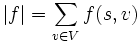
El valor del flujo es |f| = \sum_{v \in V}f(s,v)

El problema del flujo máximo trata de maximizar este flujo.

Problemas de redes de flujo

Algoritmo de flujo máximo

Tenemos el conocido problema de flujo máximo o maximal: ¿cuál es la tasa mayor a la cual el material puede ser transportado de la fuente al sumidero sin violar ninguna restricción de capacidad?

En otras palabras, el problema consiste en determinar la máxima capacidad de flujo que puede ingresar a través de la fuente y salir por el nodo de destino.

El procedimiento para obtener el flujo máximo de una red, consiste en seleccionar repetidas veces cualquier trayectoria de la fuente al destino y asignar el flujo máximo posible en esa trayectoria.

Capacidad residual: es la capacidad adicional de flujo que un arco puede llevar:
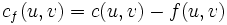
c_{f}(u,v)= c(u,v) - f(u,v) \,
  • Dada una red de flujo máximo, plantee la red residual asociada.
  • Encuentre la trayectoria de la fuente al destino con capacidad de flujo estrictamente positivo (si no existe alguno, es por que se ha encontrado el óptimo).
  • Examine estas trayectorias para encontrar la rama o arco con la menor capacidad de flujo restante e incremente en éste valor, la capacidad del flujo en sentido contrario.
  • Determine todas las trayectorias estrictamente positivas, hasta que no se permita flujo del nodo a un nodo destino.


Podemos, mediante el Algoritmo de Ford-Fulkerson, encontrar el flujo máximo de una red.

Obtenido de "Red de flujo"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Flujo sanguíneo — Saltar a navegación, búsqueda Contenido 1 Definición. 2 Introducción 2.1 Valores normales en el humano 2.2 Índice c …   Wikipedia Español

  • Flujo genético — Saltar a navegación, búsqueda El flujo genético (también conocido como migración) es la transferencia de genes de una población a otra. La migración hacia o desde una población puede ser responsable de importantes cambios en las frecuencias del… …   Wikipedia Español

  • Red de Petri — Saltar a navegación, búsqueda Una Red de Petri es una representación matemática de un sistema distribuido discreto. Las redes de Petri fueron definidas en los años 1960 por Carl Adam Petri. Son una generalización de la teoría de autómatas que… …   Wikipedia Español

  • Red de Autopistas Interestatales de Estados Unidos — Saltar a navegación, búsqueda El Sistema Nacional de Autopistas Interestatales y de Defensa Dwight D. Eisenhower , comúnmente llamado Interstate Highway System (Red de Autopistas Interestatales de Estados Unidos), es una red de autopistas libres… …   Wikipedia Español

  • Red de siguiente generación — o Red Próxima Generación (Next Generation Networking o NGN en inglés) es un amplio término que se refiere a la evolución de la actual infraestructura de redes de telecomunicación y acceso telefónico con el objetivo de lograr la congruencia de los …   Wikipedia Español

  • red — (Del lat. rete). 1. f. Aparejo hecho con hilos, cuerdas o alambres trabados en forma de mallas, y convenientemente dispuesto para pescar, cazar, cercar, sujetar, etc. 2. Labor o tejido de mallas. 3. redecilla (ǁ prenda de malla para el pelo). 4.… …   Diccionario de la lengua española

  • Red óptica síncrona — Saltar a navegación, búsqueda La Red Óptica Síncrona SONET es un estándar creado para la transmisión digital de grandes cantidades de información en redes de fibra óptica mediante el uso de láser o diodos emisores de luz LED. Este estándar,… …   Wikipedia Español

  • Red Óptica Sincrona SONET — Saltar a navegación, búsqueda La Red Óptica Síncrona, también llamada SONET, es un estándar creado para la transmisión digital de grandes cantidades de información en redes de fibra óptica mediante el uso de láser o diodos emisores de luz LED.… …   Wikipedia Español

  • Red de área de almacenamiento — Una red de área de almacenamiento, en inglés SAN (storage area network), es una red concebida para conectar servidores, matrices (arrays) de discos y librerías de soporte. Principalmente, está basada en tecnología fibre channel y más… …   Wikipedia Español

  • Red — (Del lat. rete.) ► sustantivo femenino 1 CAZA, PESCA Especie de tejido hecho con hilo, cuerda o alambres entrelazados, usado para pescar, cazar, envolver u otras cosas: ■ la red estaba repleta de peces; la pelota chocó contra la red de la pista …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”