Geometría en el Antiguo Egipto

La Geometría en el Antiguo Egipto estaba muy desarrollada, como admitieron Heródoto, Estrabón y Diodoro, comentando que los egipcios habían inventado la geometría y la habían enseñado a los griegos.

Por la naturaleza del país, cuyas inundaciones anuales les obligaba a medir periódicamente los lìmites de las parcelas cultivables, tuvieron que resolver desde muy antiguo problemas de geometría. Calculaban correctamente superficies de cuadriláteros, triángulos y tenían una buena aproximación al área del círculo.

Igual que la aritmética, era una ciencia eminentemente práctica que ofrecía soluciones concretas a diversos problemas. Los papiros de textos de matemática que han perdurado, destinados a la educación de los escribas, no dan justificación alguna de los métodos de cálculo empleados, limitándose a explicar las operaciones que hay que realizar.

Cálculo de superficies

Triángulo

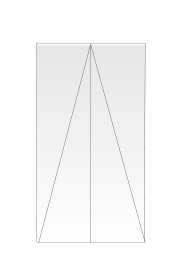
Reconstrución del procedimiento egipcio para calcular el área del triángulo.

Ese modo material de entender la ciencia se traduce en el modo en que los escribas del Imperio Medio plantean los problemas. Aparentemente, se basaban en la representación de un triángulo inscrito en un rectángulo para llegar a la conclusión: área = altura × base/2, y partían de este conocimiento para el cálculo de otras superficies como la del trapecio (Rhind, problema 52).

Ejemplo:

• papiro Rhind, problema 51:

Ejemplo del cálculo de un campo triangular. Si te dicen: Un triángulo de 10 varas de meryt (altura) y de 4 varas de base; ¿cuál es su superficie? Calcularás así:

Tomarás la mitad de 4, o sea 2, para hacerlo rectángulo. Multiplicarás 10 por 2. Es su superficie.

Operaciones:

1	400		1	1.000
1/2	200		2	2.000

Solución: Su superficie es de 2.000 codos (es decir, 2 Kha) = 20 aradas.

Círculo

El mayor éxito de los escribas egipcios fue el cálculo del área del círculo: el sistema empleado era sustraer 1/9 del diámetro y calcular la superficie del cuadrado correspondiente, lo que da un valor para π de 3'1605, cuando el resto de los pueblos de la época usaban valor 3.

Ejemplo:

• Papiro de Rhind, problema 50:

Método para calcular un trozo de tierra circular cuyo diámetro es de 10 varas. ¿Cuál es la superficie de tierra?

Debes quitar de 1 su novena parte. Quedan 8: entonces tienes que multiplicar 8 ocho veces, lo que hace 64. Mira, la superficie es 6 Kha y 4 sehat.

He aquí como se hace:

1		9
1
de eso:	1
9

Sustraes de eso, resto 8.

1	8
2	16
4	32
/8	64

Su superficie de tierra es 6 Kha (escrito 60), 4 sehat.

Cálculo de volúmenes

Los escribas calcularon los volúmenes que les interesaban, como no podía ser menos, dedicándose a la pirámide, tronco de pirámide y cilindro. (En el Imperio Medio, época de la que datan los textos conocidos, todavía se edificaban pirámides.

Pirámide

Pirámide.

No tenemos ningún ejemplo del cálculo del volumen de la pirámide, pero sí pruebas de que lo calculaban: hay un problema sobre el cálculo del ángulo de inclinación de una pendiente, un texto satírico sobre el cálculo del número exacto de ladrillos necesarios para construir una pirámide, y el hecho de calcular el volumen del tronco de pirámide:

• Papiro de Moscú, problema 14:

en resumen, se trata de averiguar el volumen de un tronco de base cuadrada, con lado de la base inferior a, lado de la superior b y altura h, los cálculos son:

elevar a al cuadrado y multiplicar el resultado por b;

elevar b al cuadrado y sumar los resultados de las tres operaciones.

dividir h entre 3 y multiplicar por el resultado de la anterior serie de operaciones: ese es el volumen.

La expresión de esta extraña serie de operaciones es la fórmula exacta del volumen del tronco de pirámide:

V = (h/3) (a² + ab + b²).

Este problema era necesario de solucionar, porque los obeliscos y muchos otros elementos arquitectónicos tenían esta forma, y convenía conocer su volumen para la extración, transporte y utilización.

cálculo del ángulo de inclinación de una pendiente

Siendo i la inclinación, B la base y h la altura. Así pues, para hallar la altura mediante la inclinación:

Cilindro

Los escribas necesitaban conocer la capacidad de los recipientes empleados en los almacenes, en su mayoría casi cilíndricos, tanto para llevar la contabilidad de lo almacenado como para pagar a los obreros y artesanos o cobrar los impuestos.
Primaba también el utilitarismo, como en todos los problemas, el estudiante no tenía más que cambiar los números para llegar al resultado correcto, en este caso el volumen dado es el área del círculo de la base (según el sistema ya visto), multiplicado por la altura del recipiente.

Véase también

• Matemáticas en el Antiguo Egipto

Bibliografía

Arnaldez, Roger y otros (1988). Las antiguas ciencias del Oriente.. Barcelona: Ediciones Orbis S.A.. ISBN 84-402-0159-1.