Pirámide (geometría)

Pirámide (geometría)

Pirámide (geometría)

Para otros usos de este término, véase Pirámide.
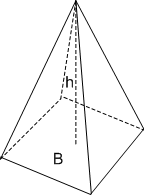Pirámide cuadrangular.
Piramide rectangular. Los vértices están marcados en naranja y las aristas en rojo. La linea amarilla una diagonal de la base.

Una pirámide es un poliedro limitado por una base, que es un polígono cualquiera; y por caras, que son triángulos y coinciden en un punto denominado ápice.

El ápice o cúspide también es llamado en ocasiones vértice de la pirámide, aunque la pirámide tiene más vértices.

Contenido

Tipos de pirámides

Una pirámide recta es un tipo de pirámide cuyas caras laterales son triángulos isósceles. En este tipo de pirámides la recta perpendicular a la base que pasa por el ápice corta a la base por su circuncentro.

Una pirámide oblícua es aquella en la que no todas sus caras laterales son triángulos isósceles.

Una pirámide regular es una pirámide recta cuya base es un polígono regular.

Una pirámide cónvexa tiene como base un polígono convexo y una pirámide cóncava tiene como base un polígono cóncavo.

Existen tres tipos de pirámides cuyas caras son triángulos equiláteros, con bases de 3, 4 y 5 lados respectivamente. Un tetraedro es una pirámide cuyas caras (base y caras laterales) son triángulos equiláteros.

Pirámides según el número de lados de su base

Las pirámides se clasifican según el número de lados de su base, que coincide con el número de caras laterales.

Número de lados de la base Tipo de pirámide Polígono que forma la base
3 Pirámide triangular Triángulo
4 Pirámide cuadrangular Cuadrado
4 Pirámide rectangular Rectángulo
5 Piramide pentagonal Pentágono
6 Piramide hexagonal Hexágono
7 Piramide heptagonal Heptágono
8 Piramide octagonal Octágono
9 Piramide eneagonal Eneágono

Área de una pirámide

Área de un polígono regular

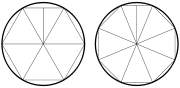Partición de polígonos regulares en triángulos isósceles.
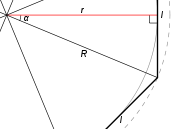La línea roja es un apotema de este octógono.

El área de un polígono regular puede calcularse en función de la longitud de cada lado y su número de lados. Un polígono regular de n lados puede dividirse en n triángulos isósceles (equiláteros en el caso del hexágono regular) cuyas bases son los lados del polígono regular. La altura de cada uno de estos triángulos es un apotema del polígono regular y divide cada uno de los triángulos isósceles en dos triángulos rectángulos, dividiendo así el polígono en 2n triángulos rectángulos.

El área del polígono regular (Ab) es igual a la suma de las áreas de los triángulos rectángulos (At):

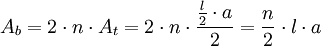
A_b = 2 \cdot n \cdot A_t = 2 \cdot n \cdot \frac{\frac{l}{2} \cdot a}{2} = \frac{n}{2} \cdot l \cdot a

Donde a es el apotema del polígono regular. Para calcular la longitud del apotema se aplica la trigonometría.

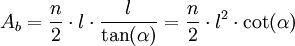
A_b = \frac{n}{2} \cdot l \cdot \frac{l}{\tan( \alpha )} = \frac{n}{2} \cdot l^2 \cdot \cot ( \alpha )

Donde α es el ángulo del vértice del triángulo rectángulo que coincide con el centro del polígono regular. El valor de este ángulo resulta de dividir el ángulo completo (2π) por el número de triángulos rectángulos (2n), luego α = 2π / 2n = π / n.

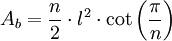
(1) A_b = \frac{n}{2} \cdot l^2 \cdot \cot \left ( \frac{\pi}{n} \right )

Área lateral de una pirámide

El área lateral de una pirámide es la suma de las áreas de las caras laterales.

En una pirámide regular, las caras laterales son triángulos isósceles. El área de cada cara es el semiproducto de su base (que es igual al lado de la base de la pirámide l ), por su altura (que es el apotema de la pirámide ap ). El área lateral de una pirámide regular resulta de multiplicar el área de una de sus caras laterales por el número de caras laterales.

(2) A_l = n \cdot \frac{l \cdot a_p}{2} = \frac{p\cdot a_p}{2}

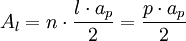
Donde ap es el apotema de la pirámide y p es el perímetro de la base.

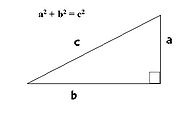Teorema de Pitágoras.
Altura de la pirámide: h = a.
Apotema de la base: ab = b.
Apotema de la pirámide: ap = c.

El apotema de la pirámide (ap) puede calcularse a partir del apotema de la base (ab) y de la altura de la pirámide (h) aplicando el teorema de Pitágoras.

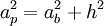
a_p^2 = a_b^2 + h^2

Área total de una pirámide

El área total de la pirámide es la suma del área de la base y el área lateral.

(3) A = Ab + Al

En el caso de una pirámide regular, sustituyendo el área de la base (1) y el área lateral (2) en la ecuación (3), se obtiene:

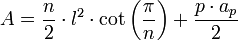
A= \frac{n}{2} \cdot l^2 \cdot \cot \left ( \frac{\pi}{n} \right ) + \frac{p\cdot a_p}{2}

Volumen

El volumen de una pirámide puede obtenerse mediante cálculo diferencial. El área de un plano de corte transversal es directamente proporcional al área de la base (Ab) y al cuadrado de la distancia del plano de corte respecto al ápice de la pirámide. Esta distancia (d) es la diferencia entre la altura de la pirámide (h) y altura del plano de corte (z).

d = h − z

Por lo tanto, el área de un plano de corte transversal situado a una altura z por encima de la base es

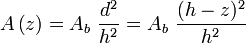
A \left(z\right) = A_b \ \frac{d^2}{h^2} = A_b \ \frac{(h - z)^2}{h^2}

El volumen de una pirámide se puede hallar conociendo el área de su base y su altura, independientemente de la forma de la base y de la posición del ápice en un plano paralelo a la base.

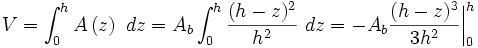
V = \int_0^h A \left(z\right)\ d z = A_b \int_0^h \frac{(h - z)^2}{h^2}\ d z = -A_b \frac{(h-z)^3}{3h^2} \bigg|_0^h

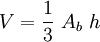
(4) V = \frac{1}{3}\ A_b \ h

Esta fórmula también es válida para el cono, ya que no depende de la forma de la base, sino de su área.

Volumen de una pirámide regular

El volumen de una pirámide cuya base es un polígono regular puede calcularse a partir del lado del polígono regular que define su base y la altura de la pirámide. Sustituyendo el área de la base Ab (1) en la ecuación del volumen de la pirámide (4) se obtiene:

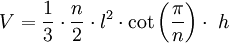
V = \frac{1}{3} \cdot \frac{n}{2} \cdot l^2 \cdot \cot \left ( \frac{\pi}{n} \right ) \cdot \ h

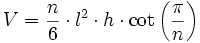
V = \frac{n}{6} \cdot l^2 \cdot h \cdot \cot \left ( \frac{\pi}{n} \right )

Centro de gravedad de una pirámide

El centro de gravedad de una pirámide de densidad uniforme está situado a una distancia de la base igual a un cuarto de su altura.[1]

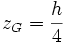
z_G = \frac{h}{4}


Referencias

  1. ↑ Vázquez, Manuel; López, Eloisa (1995), Mecánica para ingenieros, Editorial Noela, Madrid, ISBN 84-88012-03-9.

Véase también

Obtenido de "Pir%C3%A1mide (geometr%C3%ADa)"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Pirámide (geometría) — La pirámide es un cuerpo geométrico, formado por triángulos como lados, unidos todos en el mismo vértice y una base …   Enciclopedia Universal

  • Geometría molecular — Geometría de la molécula de agua. La geometría molecular o estructura molecular se refiere a la disposición tri dimensional de los átomos que constituyen una molécula. Determina muchas de las propiedades de las moléculas, como son la reactividad …   Wikipedia Español

  • Pirámide cuadrada — Saltar a navegación, búsqueda Pirámide cuadrada Tipo Johnson J92 J1 J2 Caras 4 triángulos 1 cu …   Wikipedia Español

  • Pirámide — Saltar a navegación, búsqueda La Gran Pirámide de Giza. El término pirámide puede significar: en geometría: pirámide, un cuerpo geométrico; arquitectura: pirámide, construcción con forma piramidal; economía: pirámide …   Wikipedia Español

  • Pirámide pentagonal — Saltar a navegación, búsqueda Pirámide pentagonal Tipo Johnson J1 J2 J3 Caras 5 triángulos …   Wikipedia Español

  • Pirámide cuadrada elongada — Saltar a navegación, búsqueda Pirámide cuadrada elongada Tipo Johnson J7 J8 J9 Caras …   Wikipedia Español

  • Pirámide pentagonal giroelongada — Saltar a navegación, búsqueda Pirámide pentagonal giroelongada Tipo Johnson J10 J11 J12 Caras …   Wikipedia Español

  • Geometría del espacio — La geometría del espacio es rama de la geometría que se ocupa de las propiedades y medidas de figuras geométricas en el espacio tridimensional. Entre estas figuras, también llamadas sólidos, se encuentran el cono, el cubo, el cilindro, la… …   Enciclopedia Universal

  • Pirámide cuadrada giroelongada — Saltar a navegación, búsqueda Pirámide cuadrada giroelongada Tipo Johnson J9 J10 J11 Caras …   Wikipedia Español

  • Pirámide pentagonal elongada — Saltar a navegación, búsqueda Pirámide pentagonal elongada Tipo Johnson J8 J9 J10 Caras …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”