Identidad de Euler

Este artículo o sección necesita ser wikificado con un formato acorde a las convenciones de estilo.
Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 21 de octubre de 2011.
También puedes ayudar wikificando otros artículos o cambiando este cartel por uno más específico.

Se llama identidad de Euler a un caso especial de la fórmula desarrollada por Leonhard Euler, notable por relacionar cinco números muy utilizados en la historia de las matemáticas y que pertenecen a distintas ramas.

$e^{i \pi} + 1 = 0\,\!$

donde:

π (pi) es el número más importante de la geometría^{[cita requerida]}
e (número de Euler o constante de Napier) es el número más importante del análisis matemático^{[cita requerida]}
i (imaginario) es el número más importante del álgebra^{[cita requerida]}
0 y 1 son los elementos neutros respectivamente de la adición y la multiplicación

Esta identidad se puede emplear para calcular π:

$\pi = \frac {ln(-1)}{i}\,\!$

Derivación

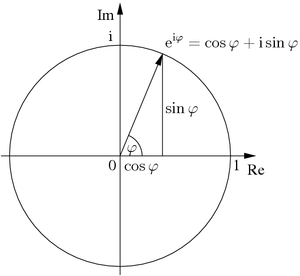
Fórmula de Euler para un ángulo general.

La identidad es un caso especial de la Fórmula de Euler, la cual especifica que

$e^{ix} = \cos x + i \sin x \,\!$

para cualquier número real x. (Nótese que los argumentos para las funciones trigonométricas sen y cos se toman en radianes.) En particular si

$x = \pi \,\!$

entonces

$e^{i \pi} = \cos \pi + i \sin \pi \,\!$

y ya que

$\cos \pi = -1 \,\!$

y que

$\sin \pi = 0 \,\!$

se sigue que

$e^{i \pi} = -1 \,\!$

Lo cual implica la identidad

$e^{i \pi} +1 = 0 \,\!$

Para una forma alternativa de notar que la identidad de Euler es tanto verdadera como profunda, supongamos que:

$x = i\pi,\,\!$

en la expansión polinomial de e a la potencia x:

$e^x = 1 + x + \frac {x^2}{2!} + \frac {x^3}{3!} + \frac {x^4}{4!} + ... ,\,\!$

para obtener:

$e^{i\pi} = 1 + i\pi + \frac {(i\pi)^2}{2!} + \frac {(i\pi)^3}{3!} + \frac {(i\pi)^4}{4!}+ ... ,\,\!$

simplificando (usando i² = -1):

$e^{i\pi} = 1 + i\pi - \frac {\pi^2}{2!} - \frac {i\pi^3}{3!} + \frac {\pi^4}{4!} + ... ,\,\!$

Al separar el lado derecho de la ecuación en subseries real e imaginarias:

$i(\pi - \frac {\pi^3}{3!} + \frac {\pi^5}{5!} - \frac {\pi^7}{7!} + ...) = 0 \quad ; \quad (1 - \frac {\pi^2}{2!} + \frac {\pi^4}{4!} - \frac {\pi^6}{6!} + ...) = -1\!$

Se puede comprobar la convergencia de estas dos subseries infinitas, lo cual implica

$e^{i \pi} = -1\,\!$

Logaritmos de números negativos

Durante la historia ha habido disputas sobre cómo calcular los logaritmos de números negativos. Gracias a la identidad de Euler, dicha disputa ha sido zanjada. Si queremos calcular, por ejemplo, $l o g ( - 4)$ podemos proceder de la siguiente manera:

$log(-4) \!$

$log(-1) + log(4) \!$

$\ln(-1)/2,3026 + log(4) \!$

Sabiendo que $l n ( - 1) = π i$ :

$\pi i/2,3026 + log(4) \!$

Referencias

Crease, Robert P., "The greatest equations ever", PhysicsWeb, October 2004 (registration required).
Crease, Robert P. "Equations as icons," PhysicsWeb, March 2007 (registration required).
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (New York: Penguin, 2004).
Kasner, E., and Newman, J., Mathematics and the Imagination (Bell and Sons, 1949).
Maor, Eli, e: The Story of a number (Princeton University Press, 1998), ISBN 0-691-05854-7
Nahin, Paul J., Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills (Princeton University Press, 2006), ISBN 978-0-691-11822-2
Reid, Constance, From Zero to Infinity (Mathematical Association of America, various editions).
Sandifer, Ed, "Euler's Greatest Hits", MAA Online, February 2007.
Jayadev, C, "The Greatest equation ever"
Weisstein, Eric W.. «Euler Formula» (en inglés). MathWorld--A Wolfram Web Resource. Consultado el 15-05-2009.

Véase también

Enlaces externos

Demostración completa de la identidad de Euler

Categorías:

Π
Análisis matemático
Identidad matemática
Exponenciales

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать курсовую

Mira otros diccionarios:

Identidad de Euler — La fórmula : llamada identidad de Euler, es ciertamente la fórmula más importante de las matemáticas, pues une de forma escueta (y misteriosa) distintos campos de esta ciencia: ● p es el número mas importante de la geometría. ● e es el número mas … Enciclopedia Universal
Identidad de los cuatro cuadrados de Euler — Este artículo o sección tiene el primer párrafo que usa términos técnicos sin explicación para los lectores interesados en el tema. Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los… … Wikipedia Español
Identidad de Brahmagupta — En matemática, la identidad de Brahmagupta enuncia que el producto de dos números, cada uno de los cuales es la suma de dos cuadrados, también es la suma de dos cuadrados. Específicamente: La identidad es cierta en cualquier anillo conmutativo,… … Wikipedia Español
Identidad de Brahmagupta — En matemáticas, la identidad de Brahmagupta enuncia que el producto de dos números, cada uno de los cuales es la suma de dos cuadrados, también es la suma de dos cuadrados. Específicamente: La identidad es cierta en cualquier anillo conmutativo,… … Enciclopedia Universal
Leonhard Euler — Retrato de Leonhard Euler, pintado por Johann Georg Bruck … Wikipedia Español
Fórmula de Euler — La fórmula o relación de Euler, atribuida a Leonhard Euler, establece que: para todo número real x. Aquí, e es la base del logaritmo natural, i es la unidad imaginaria, sin x y cos x son funciones trigonométricas. O bien: siendo z la… … Wikipedia Español
Ecuaciones de Euler — Saltar a navegación, búsqueda En diversas áreas de la mecánica y las matemáticas existen diversas ecuaciones de Euler: En mecánica de fluidos tenemos las Ecuaciones de Euler (fluidos) para fluidos compresibles. En Mecánica del sólido rígido… … Wikipedia Español
Ecuaciones de Euler — Esta página trata sobre el flujo de fluidos compresibles. Otras páginas relacionadas con los trabajos de Euler son fórmula de Euler e Identidad de Euler. En dinámica de fluidos, las ecuaciones de Euler son las que gobiernan el movimiento de un… … Enciclopedia Universal
Fracción continua de Euler — Saltar a navegación, búsqueda En teoría analítica de fracciones continuas, la fracción continua de Euler es una identidad que conecta una clase general de series infinitas con una fracción continua infinita. Publicada por primera vez en 1748, fue … Wikipedia Español
Teorema de rotación de Euler — En geometría el Teorema de la rotación de Euler dice que, en un espacio tridimensional, cualquier movimiento de un sólido rígido que mantenga un punto constante, también debe dejar constante un eje completo. Esto también quiere decir que… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Identidad de Euler

Contenido

Derivación

Logaritmos de números negativos

Referencias

Véase también

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Identidad de Euler

Contenido

Derivación

Logaritmos de números negativos

Referencias

Véase también

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo