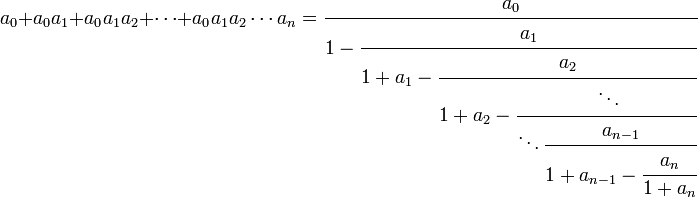Fracción continua de Euler

Fracción continua de Euler

Fracción continua de Euler

En teoría analítica de fracciones continuas, la fracción continua de Euler es una identidad que conecta una clase general de series infinitas con una fracción continua infinita. Publicada por primera vez en 1748, fue considerada en un principio como una identidad simple que conectaba una suma de términos finitos con una fracción continua finita, donde la extensión al caso infinito aparecía inmediatamente. Actualmente, es una muy apreciada y útil herramienta en desarrollos analíticos en el problema de la convergencia general para fracciones continuas infinitas con elementos complejos.

Contenido

Formulación original

Leonhard Euler obtuvo la fórmula como una identidad que conecta una suma finita de productos con una fracción continua finita como:

a_0 + a_0a_1 + a_0a_1a_2 + \cdots + a_0a_1a_2\cdots a_n = \cfrac{a_0}{1 - \cfrac{a_1}{1 + a_1 - \cfrac{a_2}{1 + a_2 - \cfrac{\ddots}{\ddots \cfrac{a_{n-1}}{1 + a_{n-1} - \cfrac{a_n}{1 + a_n}}}}}}\,

La identidad puede ser fácilmente obtenida mediante inducción en n, y por lo tanto, también aplicable en el caso límite: si la expresión de la parte izquierda tiende a expresarse como una serie convergente infinita, la expresión de la derecha también tenderá a expresarse como una fracción continua infinita convergente.

Notación moderna

Si

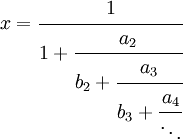
x = \cfrac{1}{1 + \cfrac{a_2}{b_2 + \cfrac{a_3}{b_3 + \cfrac{a_4}{\ddots}}}}\,

es una fracción continua con elementos complejos, y ninguno de los denominadores Bi son cero, una secuencia de ratios {ri} puede ser definida por:

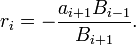
r_i = -\frac{a_{i+1}B_{i-1}}{B_{i+1}}.\,


Para un x y un ri así definidos, las siguientes igualdades pueden demostrarse por inducción.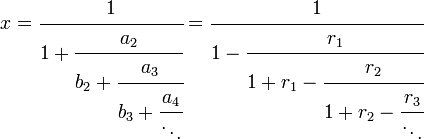

x = \cfrac{1}{1 + \cfrac{a_2}{b_2 + \cfrac{a_3}{b_3 + \cfrac{a_4}{\ddots}}}} = \cfrac{1}{1 - \cfrac{r_1}{1 + r_1 - \cfrac{r_2}{1 + r_2 - \cfrac{r_3}{\ddots}}}}\,

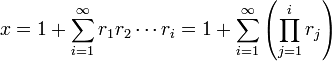
x = 1 + \sum_{i=1}^\infty r_1r_2\cdots r_i = 1 + \sum_{i=1}^\infty \left( \prod_{j=1}^i r_j \right)\,

Esta igualdad se puede entender como una equivalencia, en el sentido de que la n-esimo término convergente de cada fracción continua es igual a la n-ésima suma parcial de la serie mostrada arriba. Así, si esa serie es convergente o uniformemente convergente, cuando los ai y bi son funciones de variable compleja z, entonces las fracciones continuas equivalentes también convergen, o convergen uniformemente.[1]

Véase también

Referencias

  1. ↑ (Wall, 1948, p. 17)
Obtenido de "Fracci%C3%B3n continua de Euler"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Fracción continua generalizada — Saltar a navegación, búsqueda En análisis complejo, una rama de las matemáticas, una fracción continua generalizada o fracción fractal es una generalización de una fracción continua en la cual los numeradores parciales y los denominadores… …   Wikipedia Español

  • Fracción continua — Saltar a navegación, búsqueda En matemáticas, una fracción continua es una expresión de la forma: donde a0 es un entero y todos los demás números an son enteros positivos. Si se permite que los numeradores o los denominadores parciales tomen… …   Wikipedia Español

  • Fracción continua de Gauss — Saltar a navegación, búsqueda En análisis complejo la fracción continua de Gauss es un caso particular de fracción continua generalizada derivada de la serie hipergeométrica. Fue una de las primeras fracciones continuas analíticas conocidas en… …   Wikipedia Español

  • Constante de Euler-Mascheroni — La constante de Euler Mascheroni, (también conocida como constante de Euler ) es una constante matemática que aparece principalmente en teoría de números, y se denota con la letra griega minúscula γ (Gamma). Se define como el límite de la… …   Wikipedia Español

  • Leonhard Euler — Retrato de Leonhard Euler, pintado por Johann Georg Bruck …   Wikipedia Español

  • Número e — e} es el único número a, tal que la derivada de la función exponencial f(x) = ax (curva azul) en el punto x = 0 es igual a 1. En comparación, las funciones 2x (curva a puntos) y 4x (curva a trazos) son mostradas; no son tangentes a la… …   Wikipedia Español

  • Número π — π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El… …   Wikipedia Español

  • Demostración de la irracionalidad de π — Saltar a navegación, búsqueda Símbolo del número π, popularizado por Leonhard Euler. Aunque la constante matemática conocida como π (pi) ha sido estudiada desde la antigüedad, y también el concepto de número irracional, no fue sin …   Wikipedia Español

  • Transformada binomial — En matemáticas, en el campo de la combinatoria, la transformada binomial es una transformación de sucesiones, o sea, una transformación de una sucesión, que se obtiene calculando sus diferencias anteriores. Esta relacionada con la transformada de …   Wikipedia Español

  • Raíz cuadrada de 2 — La raíz cuadrada de 2 es igual a la longitud de la hipotenusa de un triángulo rectángulo cuyos catetos tienen una longitud 1. La raíz cuadrada de 2, también conocida como constante pitagórica, se denota a menudo como: es un …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”