- Lema de Reynolds
-
Lema de Reynolds
El Lema de Reynolds introducido por el ingeniero irlandés Osborne Reynolds que demuestra que la variación de flujo de una propiedad es igual a la variación de la propiedad dentro del flujo:
Demostración
Sea A una cierta propiedad genérica (escalar, vectorial o tensorial) de un medio continuo, y sea ψ(x, t ) la cantidad de esta propiedad A por unidad de masa. Por consiguiente, ρψ(x,t) es la cantidad de la propiedad por unidad de volumen.
Consideremos un volumen material arbitrario de medio continuo que en el instante t ocupa en el espacio un volumen V. La cantidad de la propiedad genérica A en el volumen material V en el instante t será:Donde ψ es la propiedad a estudiar
La variación a lo largo del tiempo del contenido de la propiedad A en el volumen material V vendrá dada por la derivada temporal de Q(t) , que utilizando la expresión de la derivada material de una integral de volumen será:
Utilizando la expresión para la derivada material de un producto de funciones, agrupando términos y utilizando la ecuación de continuidad:
Como
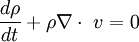por continuidad, se llega a la conclusión de que:Categoría: Teoremas -
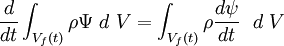
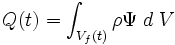
![\ Q'(t) =\frac{d}{dt}\int_{V_f(t)}\rho\Psi\; d\ V =\int_{V_f(t)} [\frac{d\rho\psi}{dt}\ +\rho\psi\nabla\cdot\ v ]\; d\ V](/pictures/eswiki/57/9ebd83a56635f8a488883198f48253a4.png)
![\frac{d}{dt}\int_{V_f(t)}\rho\Psi\; d\ V =\int_{V_f(t)} [\rho\frac{d\psi}{dt}\ + \psi\frac{d\rho}{dt} +\rho\psi\nabla\cdot\ v ]\; d\ V](/pictures/eswiki/48/05970d68d8410e3bd55c117a2a961155.png)
![=\int_{V_f(t)} [\rho\frac{d\psi}{dt}\ + \psi [\frac{d\rho}{dt} +\rho\nabla\cdot\ v ]]\; d\ V](/pictures/eswiki/101/ee982531fdcf1c4d58ad54c03cbcd431.png)
Wikimedia foundation. 2010.
