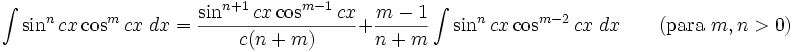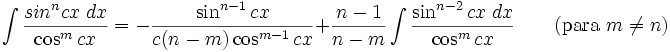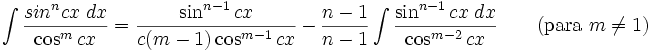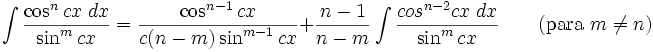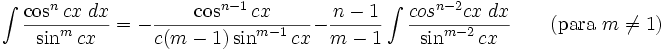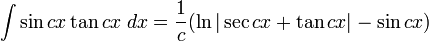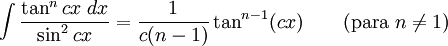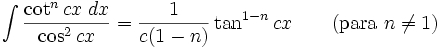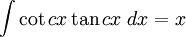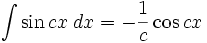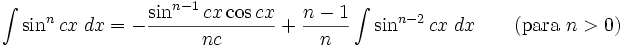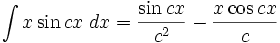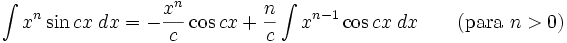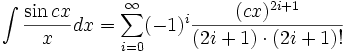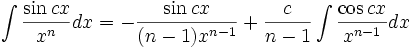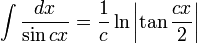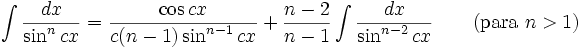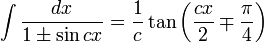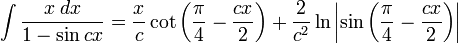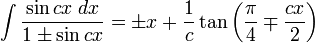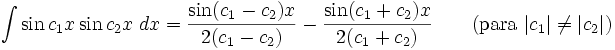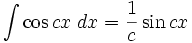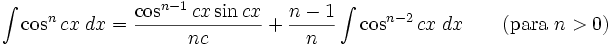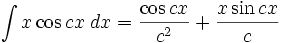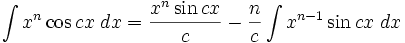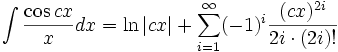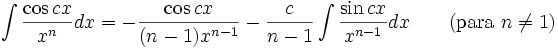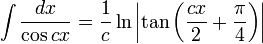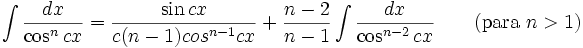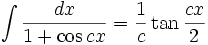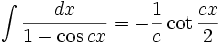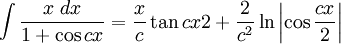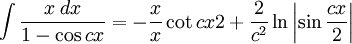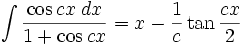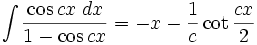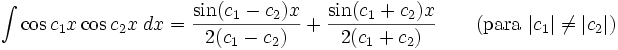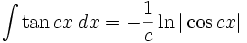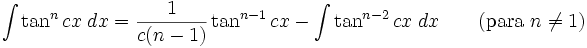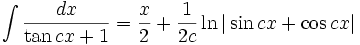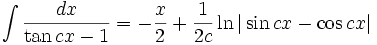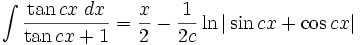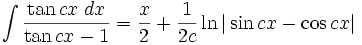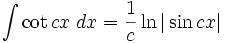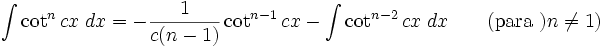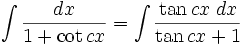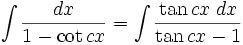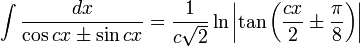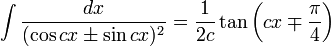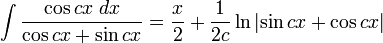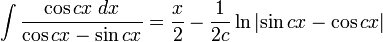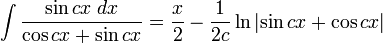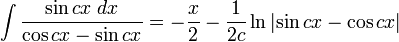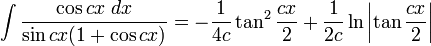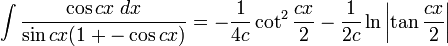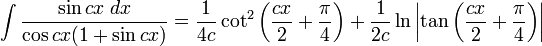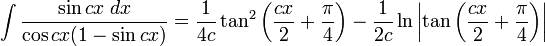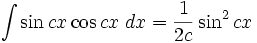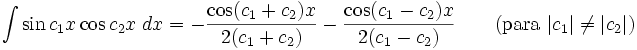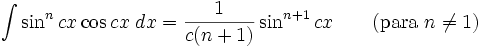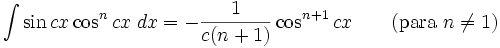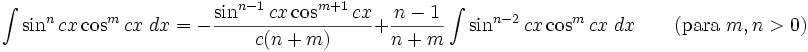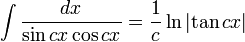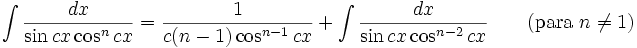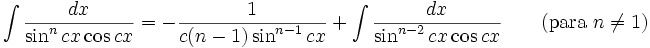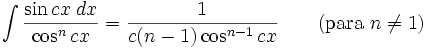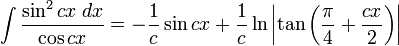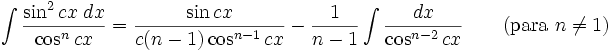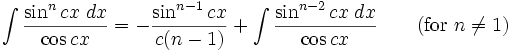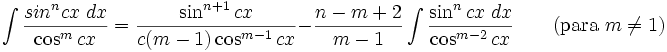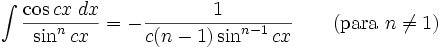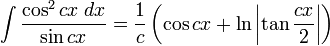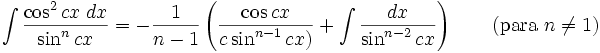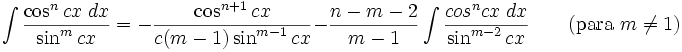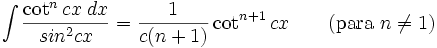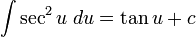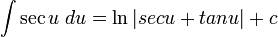Integrales de funciones trigonométricas

Integrales de funciones trigonométricas

Anexo:Integrales de funciones trigonométricas

La siguiente es una lista de integrales de funciones trigonométricas.

Contenido

Integrales que contienen solamente seno

\int\sin cx\;dx = -\frac{1}{c}\cos cx
\int\sin^n cx\;dx = -\frac{\sin^{n-1} cx\cos cx}{nc} + \frac{n-1}{n}\int\sin^{n-2} cx\;dx \qquad\mbox{(para }n>0\mbox{)}
\int x\sin cx\;dx = \frac{\sin cx}{c^2}-\frac{x\cos cx}{c}
\int x^n\sin cx\;dx = -\frac{x^n}{c}\cos cx+\frac{n}{c}\int x^{n-1}\cos cx\;dx \qquad\mbox{(para }n>0\mbox{)}
\int\frac{\sin cx}{x} dx = \sum_{i=0}^\infty (-1)^i\frac{(cx)^{2i+1}}{(2i+1)\cdot (2i+1)!}
\int\frac{\sin cx}{x^n} dx = -\frac{\sin cx}{(n-1)x^{n-1}} + \frac{c}{n-1}\int\frac{\cos cx}{x^{n-1}} dx
\int\frac{dx}{\sin cx} = \frac{1}{c}\ln\left|\tan\frac{cx}{2}\right|
\int\frac{dx}{\sin^n cx} = \frac{\cos cx}{c(n-1) \sin^{n-1} cx}+\frac{n-2}{n-1}\int\frac{dx}{\sin^{n-2}cx} \qquad\mbox{(para }n>1\mbox{)}
\int\frac{dx}{1\pm\sin cx} = \frac{1}{c}\tan\left(\frac{cx}{2}\mp\frac{\pi}{4}\right)


\int\frac{x\;dx}{1-\sin cx} = \frac{x}{c}\cot\left(\frac{\pi}{4} - \frac{cx}{2}\right)+\frac{2}{c^2}\ln\left|\sin\left(\frac{\pi}{4}-\frac{cx}{2}\right)\right|
\int\frac{\sin cx\;dx}{1\pm\sin cx} = \pm x+\frac{1}{c}\tan\left(\frac{\pi}{4}\mp\frac{cx}{2}\right)
\int\sin c_1x\sin c_2x\;dx = \frac{\sin(c_1-c_2)x}{2(c_1-c_2)}-\frac{\sin(c_1+c_2)x}{2(c_1+c_2)} \qquad\mbox{(para }|c_1|\neq|c_2|\mbox{)}

Integrales que contienen solamente cos

\int\cos cx\;dx = \frac{1}{c}\sin cx
\int\cos^n cx\;dx = \frac{\cos^{n-1} cx\sin cx}{nc} + \frac{n-1}{n}\int\cos^{n-2} cx\;dx \qquad\mbox{(para }n>0\mbox{)}
\int x\cos cx\;dx = \frac{\cos cx}{c^2} + \frac{x\sin cx}{c}
\int x^n\cos cx\;dx = \frac{x^n\sin cx}{c} - \frac{n}{c}\int x^{n-1}\sin cx\;dx
\int\frac{\cos cx}{x} dx = \ln|cx|+\sum_{i=1}^\infty (-1)^i\frac{(cx)^{2i}}{2i\cdot(2i)!}
\int\frac{\cos cx}{x^n} dx = -\frac{\cos cx}{(n-1)x^{n-1}}-\frac{c}{n-1}\int\frac{\sin cx}{x^{n-1}} dx \qquad\mbox{(para }n\neq 1\mbox{)}
\int\frac{dx}{\cos cx} = \frac{1}{c}\ln\left|\tan\left(\frac{cx}{2}+\frac{\pi}{4}\right)\right|
\int\frac{dx}{\cos^n cx} = \frac{\sin cx}{c(n-1) cos^{n-1} cx} + \frac{n-2}{n-1}\int\frac{dx}{\cos^{n-2} cx} \qquad\mbox{(para }n>1\mbox{)}
\int\frac{dx}{1+\cos cx} = \frac{1}{c}\tan\frac{cx}{2}
\int\frac{dx}{1-\cos cx} = -\frac{1}{c}\cot\frac{cx}{2}
\int\frac{x\;dx}{1+\cos cx} = \frac{x}{c}\tan{cx}{2} + \frac{2}{c^2}\ln\left|\cos\frac{cx}{2}\right|
\int\frac{x\;dx}{1-\cos cx} = -\frac{x}{x}\cot{cx}{2}+\frac{2}{c^2}\ln\left|\sin\frac{cx}{2}\right|
\int\frac{\cos cx\;dx}{1+\cos cx} = x - \frac{1}{c}\tan\frac{cx}{2}
\int\frac{\cos cx\;dx}{1-\cos cx} = -x-\frac{1}{c}\cot\frac{cx}{2}
\int\cos c_1x\cos c_2x\;dx = \frac{\sin(c_1-c_2)x}{2(c_1-c_2)}+\frac{\sin(c_1+c_2)x}{2(c_1+c_2)} \qquad\mbox{(para }|c_1|\neq|c_2|\mbox{)}

Texto de titular

Integrales que contienen solamente tan

\int\tan cx\;dx = -\frac{1}{c}\ln|\cos cx|
\int\tan^n cx\;dx = \frac{1}{c(n-1)}\tan^{n-1} cx-\int\tan^{n-2} cx\;dx \qquad\mbox{(para }n\neq 1\mbox{)}
\int\frac{dx}{\tan cx + 1} = \frac{x}{2} + \frac{1}{2c}\ln|\sin cx + \cos cx|
\int\frac{dx}{\tan cx - 1} = -\frac{x}{2} + \frac{1}{2c}\ln|\sin cx - \cos cx|
\int\frac{\tan cx\;dx}{\tan cx + 1} = \frac{x}{2} - \frac{1}{2c}\ln|\sin cx + \cos cx|
\int\frac{\tan cx\;dx}{\tan cx - 1} = \frac{x}{2} + \frac{1}{2c}\ln|\sin cx - \cos cx|

Integrales que contienen solamente cot

\int\cot cx\;dx = \frac{1}{c}\ln|\sin cx|
\int\cot^n cx\;dx = -\frac{1}{c(n-1)}\cot^{n-1} cx - \int\cot^{n-2} cx\;dx \qquad\mbox{(para )}n\neq 1\mbox{)}
\int\frac{dx}{1 + \cot cx} = \int\frac{\tan cx\;dx}{\tan cx+1}
\int\frac{dx}{1 - \cot cx} = \int\frac{\tan cx\;dx}{\tan cx-1}

Integrales que contienen sin y cos

\int\frac{dx}{\cos cx\pm\sin cx} = \frac{1}{c\sqrt{2}}\ln\left|\tan\left(\frac{cx}{2}\pm\frac{\pi}{8}\right)\right|
\int\frac{dx}{(\cos cx\pm\sin cx)^2} = \frac{1}{2c}\tan\left(cx\mp\frac{\pi}{4}\right)
\int\frac{\cos cx\;dx}{\cos cx + \sin cx} = \frac{x}{2} + \frac{1}{2c}\ln\left|\sin cx + \cos cx\right|
\int\frac{\cos cx\;dx}{\cos cx - \sin cx} = \frac{x}{2} - \frac{1}{2c}\ln\left|\sin cx - \cos cx\right|
\int\frac{\sin cx\;dx}{\cos cx + \sin cx} = \frac{x}{2} - \frac{1}{2c}\ln\left|\sin cx + \cos cx\right|
\int\frac{\sin cx\;dx}{\cos cx - \sin cx} = -\frac{x}{2} - \frac{1}{2c}\ln\left|\sin cx - \cos cx\right|
\int\frac{\cos cx\;dx}{\sin cx(1+\cos cx)} = -\frac{1}{4c}\tan^2\frac{cx}{2}+\frac{1}{2c}\ln\left|\tan\frac{cx}{2}\right|
\int\frac{\cos cx\;dx}{\sin cx(1+-\cos cx)} = -\frac{1}{4c}\cot^2\frac{cx}{2}-\frac{1}{2c}\ln\left|\tan\frac{cx}{2}\right|
\int\frac{\sin cx\;dx}{\cos cx(1+\sin cx)} = \frac{1}{4c}\cot^2\left(\frac{cx}{2}+\frac{\pi}{4}\right)+\frac{1}{2c}\ln\left|\tan\left(\frac{cx}{2}+\frac{\pi}{4}\right)\right|
\int\frac{\sin cx\;dx}{\cos cx(1-\sin cx)} = \frac{1}{4c}\tan^2\left(\frac{cx}{2}+\frac{\pi}{4}\right)-\frac{1}{2c}\ln\left|\tan\left(\frac{cx}{2}+\frac{\pi}{4}\right)\right|
\int\sin cx\cos cx\;dx = \frac{1}{2c}\sin^2 cx
\int\sin c_1x\cos c_2x\;dx = -\frac{\cos(c_1+c_2)x}{2(c_1+c_2)}-\frac{\cos(c_1-c_2)x}{2(c_1-c_2)} \qquad\mbox{(para }|c_1|\neq|c_2|\mbox{)}
\int\sin^n cx\cos cx\;dx = \frac{1}{c(n+1)}\sin^{n+1} cx \qquad\mbox{(para }n\neq 1\mbox{)}
\int\sin cx\cos^n cx\;dx = -\frac{1}{c(n+1)}\cos^{n+1} cx \qquad\mbox{(para }n\neq 1\mbox{)}
\int\sin^n cx\cos^m cx\;dx = -\frac{\sin^{n-1} cx\cos^{m+1} cx}{c(n+m)}+\frac{n-1}{n+m}\int\sin^{n-2} cx\cos^m cx\;dx \qquad\mbox{(para }m,n>0\mbox{)}
también: \int\sin^n cx\cos^m cx\;dx = \frac{\sin^{n+1} cx\cos^{m-1} cx}{c(n+m)} + \frac{m-1}{n+m}\int\sin^n cx\cos^{m-2} cx\;dx \qquad\mbox{(para }m,n>0\mbox{)}
\int\frac{dx}{\sin cx\cos cx} = \frac{1}{c}\ln\left|\tan cx\right|
\int\frac{dx}{\sin cx\cos^n cx} = \frac{1}{c(n-1)\cos^{n-1} cx}+\int\frac{dx}{\sin cx\cos^{n-2} cx} \qquad\mbox{(para }n\neq 1\mbox{)}
\int\frac{dx}{\sin^n cx\cos cx} = -\frac{1}{c(n-1)\sin^{n-1} cx}+\int\frac{dx}{\sin^{n-2} cx\cos cx} \qquad\mbox{(para }n\neq 1\mbox{)}
\int\frac{\sin cx\;dx}{\cos^n cx} = \frac{1}{c(n-1)\cos^{n-1} cx} \qquad\mbox{(para }n\neq 1\mbox{)}
\int\frac{\sin^2 cx\;dx}{\cos cx} = -\frac{1}{c}\sin cx+\frac{1}{c}\ln\left|\tan\left(\frac{\pi}{4}+\frac{cx}{2}\right)\right|
\int\frac{\sin^2 cx\;dx}{\cos^n cx} = \frac{\sin cx}{c(n-1)\cos^{n-1}cx}-\frac{1}{n-1}\int\frac{dx}{\cos^{n-2}cx} \qquad\mbox{(para }n\neq 1\mbox{)}
\int\frac{\sin^n cx\;dx}{\cos cx} = -\frac{\sin^{n-1} cx}{c(n-1)} + \int\frac{\sin^{n-2} cx\;dx}{\cos cx} \qquad\mbox{(for }n\neq 1\mbox{)}
\int\frac{sin^n cx\;dx}{\cos^m cx} = \frac{\sin^{n+1} cx}{c(m-1)\cos^{m-1} cx}-\frac{n-m+2}{m-1}\int\frac{\sin^n cx\;dx}{\cos^{m-2} cx} \qquad\mbox{(para }m\neq 1\mbox{)}
también: \int\frac{sin^n cx\;dx}{\cos^m cx} = -\frac{\sin^{n-1} cx}{c(n-m)\cos^{m-1} cx}+\frac{n-1}{n-m}\int\frac{\sin^{n-2} cx\;dx}{\cos^m cx} \qquad\mbox{(para }m\neq n\mbox{)}
también: \int\frac{sin^n cx\;dx}{\cos^m cx} = \frac{\sin^{n-1} cx}{c(m-1)\cos^{m-1} cx}-\frac{n-1}{n-1}\int\frac{\sin^{n-1} cx\;dx}{\cos^{m-2} cx} \qquad\mbox{(para }m\neq 1\mbox{)}
\int\frac{\cos cx\;dx}{\sin^n cx} = -\frac{1}{c(n-1)\sin^{n-1} cx} \qquad\mbox{(para }n\neq 1\mbox{)}
\int\frac{\cos^2 cx\;dx}{\sin cx} = \frac{1}{c}\left(\cos cx+\ln\left|\tan\frac{cx}{2}\right|\right)
\int\frac{\cos^2 cx\;dx}{\sin^n cx} = -\frac{1}{n-1}\left(\frac{\cos cx}{c\sin^{n-1} cx)}+\int\frac{dx}{\sin^{n-2} cx}\right) \qquad\mbox{(para }n\neq 1\mbox{)}
\int\frac{\cos^n cx\;dx}{\sin^m cx} = -\frac{\cos^{n+1} cx}{c(m-1)\sin^{m-1} cx} - \frac{n-m-2}{m-1}\int\frac{cos^n cx\;dx}{\sin^{m-2} cx} \qquad\mbox{(para }m\neq 1\mbox{)}
también: \int\frac{\cos^n cx\;dx}{\sin^m cx} = \frac{\cos^{n-1} cx}{c(n-m)\sin^{m-1} cx} + \frac{n-1}{n-m}\int\frac{cos^{n-2} cx\;dx}{\sin^m cx} \qquad\mbox{(para }m\neq n\mbox{)}
también: \int\frac{\cos^n cx\;dx}{\sin^m cx} = -\frac{\cos^{n-1} cx}{c(m-1)\sin^{m-1} cx} - \frac{n-1}{m-1}\int\frac{cos^{n-2} cx\;dx}{\sin^{m-2} cx} \qquad\mbox{(para }m\neq 1\mbox{)}

çüÁμνΞ=== Integrales que contienen sin y tan === \int \sin cx \tan cx\;dx = \frac{1}{c}(\ln|\sec cx + \tan cx| - \sin cx)\,\!

\int\frac{\tan^n cx\;dx}{\sin^2 cx} = \frac{1}{c(n-1)} \tan^{n-1} (cx) \qquad\mbox{(para }n\neq 1\mbox{)}\,\!

Integrales que contienen cos y tan

No se pudo entender (error léxico): \int\frac{\tan^n cx\;dx}{\cos^2 cx} = \frac{<math>Escribe xzx aquí una fórmula

1}{c(n+1)}\tan^{n+1} cx \qquad\mbox{(para }n\neq 1\mbox{)}</math>

Integrales que contienen sin y cot

\int\frac{\cot^n cx\;dx}{sin^2 cx} = \frac{1}{c(n+1)}\cot^{n+1} cx \qquad\mbox{(para }n\neq 1\mbox{)}

Integrales que contienen cos y cot

\int\frac{\cot^n cx\;dx}{\cos^2 cx} = \frac{1}{c(1-n)}\tan^{1-n} cx \qquad\mbox{(para }n\neq 1\mbox{)}\,\!


Integrales que contienen tan y cot

\int \cot cx \tan cx\;dx = x\

Integral de la Sec

\int\sec^2 u\;du = \tan u+c
\int\sec u\;du = \ln |sec u + tan u |+c
Obtenido de "Anexo:Integrales de funciones trigonom%C3%A9tricas"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Anexo:Integrales de funciones trigonométricas — La siguiente es una lista de integrales de funciones trigonométricas y su correspondiente simplificación. Contenido 1 Integrales que contienen solamente sen 2 Integrales que contienen solamente cos 3 Integrales que contienen solamente tan …   Wikipedia Español

  • Lista de integrales de funciones trigonométricas — La siguiente es una lista de integrales de funciones trigonométricas …   Enciclopedia Universal

  • Integrales de funciones inversas trigonométricas — Anexo:Integrales de funciones inversas trigonométricas Saltar a navegación, búsqueda La siguiente es una lista de integrales de funciones inversas trigonométricas …   Wikipedia Español

  • Anexo:Integrales de funciones inversas trigonométricas — La siguiente es una lista de integrales de funciones inversas trigonométricas …   Wikipedia Español

  • Lista de integrales de funciones inversas trigonométricas — La siguiente es una lista de integrales de funciones inversas trigonométricas …   Enciclopedia Universal

  • Integrales — Anexo:Integrales Saltar a navegación, búsqueda Lista de integrales según el tipo de función: Lista de integrales de funciones racionales Lista de integrales de funciones irracionales Lista de integrales de funciones trigonométricas Lista de… …   Wikipedia Español

  • Anexo:Integrales — Lista de integrales según el tipo de función: Lista de integrales de funciones racionales Lista de integrales de funciones irracionales Lista de integrales de funciones trigonométricas Lista de integrales de funciones hiperbólicas Lista de… …   Wikipedia Español

  • Lista de integrales — según el tipo de función: ● Lista de integrales de funciones racionales ● Lista de integrales de funciones irracionales ● Lista de integrales de funciones trigonométricas ● Lista de integrales de funciones hiperbólicas ● Lista de integrales de… …   Enciclopedia Universal

  • Anexo:Funciones matemáticas — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Fórmulas de reducción para integrales — Anexo:Fórmulas de reducción para integrales Saltar a navegación, búsqueda En ocasiones la integración definida o indefinida de funciones de una variable se facilita mediante las llamadas fórmulas de reducción. Son éstas una cierta forma de poner… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”