Raíz cuadrada de 2

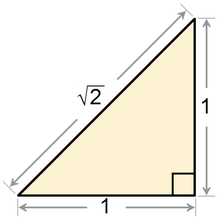La raíz cuadrada de 2 es igual a la longitud de la hipotenusa de un triángulo rectángulo cuyos catetos tienen una longitud 1.

La raíz cuadrada de 2, también conocida como constante pitagórica, se denota a menudo como:

$\sqrt{2} \,$

es un número real positivo que multiplicado por sí mismo da el número 2. Su valor numérico aproximado a 75 posiciones decimales (sucesión A002193 en OEIS) es:^[1]

1,414213562373095048801688724209698078569671875376948073176679737990732478462

La raíz cuadrada de 2 fue posiblemente el primer número irracional conocido. Geométricamente es la longitud de la diagonal de un cuadrado de longitud unidad; el valor de la longitud de esta diagonal se puede averiguar mediante el Teorema de Pitágoras. En la época en las que los ordenadores no eran tan baratos (antes de la función SQRT) la aproximación fraccional más rápida era 99/70 (difiere del valor correcto menos de 1/10 000 y es mejor que la aproximación racional de 22/7 para π).

La razón plateada se define como : $\scriptstyle{1+\sqrt{2}}$ .

Historia

Las tablas babilónicas del (YBC 7289) (c. 2000–1650 a. C.) proporcionan una aproximación de $\sqrt{2}$ en cuatro dígitos sexagesimales, que es similar a seis cifras decimales:^[2]

$1 + \frac{24}{60} + \frac{51}{60^2} + \frac{10}{60^3} = 1,41421\overline{296}$ .

Otra aproximación antigua a este número irracional se da en la antigua India por los textos matemáticos, el Sulbasutras (c. 800—200 a. C.) diciendo: Incrementa la longitud [del lado] por su tercera parte, y su tercera por su tres cuartas y su tercera por su treinta y cuatroava parte de cuatro.^[3] Esto es

$1 + \frac{1}{3} + \frac{1}{3 \cdot 4} - \frac{1}{3 \cdot4 \cdot 34} = \frac{577}{408} \approx 1,414215686.$

El descubrimiento de la raíz cuadrada de 2 como un número irracional se atribuye generalmente al pitagórico Hipaso de Metaponto, quien fue el primero en producir la demostración (vía demostración geométrica) de la irracionalidad. La historia narra que precisamente descubrió la irracionalidad de la raíz de 2 cuando intentaba averiguar una expresión racional del mismo. Sin embargo Pitágoras creía en la definición absoluta de los números como media, y esto le obligaba a no creer en la existencia de los números irracionales. Por esta razón estuvo ya desde el principio en contra de esa demostración, por esta razón fue sentenciado a la pena capital por sus compañeros pitagóricos.

Algoritmo computacional

Existe una gran cantidad de algoritmos empleados la aproximación de la raíz cuadrada de 2. El más común de los algoritmos para averiguar una aproximación en computadores o calculadoras es el denominado método babilónico^[4] de cálculo de las raíces cuadradas, siendo éste uno de los muchos empleados para el cálculo de raíces cuadradas. Funciona como sigue:

Se toma en primer lugar un valor arbitrario, que denominaremos, $F 0$ ; esta primera aproximación importa poco, es considerada sólo como un punto de comienzo del algoritmo y afecta en cuantas iteraciones debe hacer el algoritmo hasta alcanzar la aproximación con una precisión requerida. Entonces, empleando esta suposición inicial, se procede a iterar mediante la siguiente cómputo recursivo:

$F_{n+1} = \frac{F_n + \frac{2}{F_n}}{2}$

Cuanto más iteraciones se hagan mediante este algoritmo (es decir más cálculos con un valor de n grande), se obtendrá una mejor aproximación del valor real de raíz cuadrada de 2.

El valor de $\sqrt{2}$ ha sido calculado hasta 137.438.953.444 posiciones decimales por el equipo de Yasumasa Kanada en el año 1997. Entre las constantes matemáticas con cifras no periódicas, sólo π ha sido calculado con mayor precisión.^[5]

Pruebas de irracionalidad

Existen varias pruebas de la irracionalidad de $\scriptstyle{\sqrt{2}}$ basadas en el método del descenso infinito y en el método de reducción al absurdo, que se fundamenta en suponer que $\scriptstyle{\sqrt{2}}$ es un número racional y llegar, utilizando razonamientos rigurosamente correctos, a una contradicción, lo que hace concluir que la primera suposición tiene que ser falsa.

Prueba geométrica

Se fundamenta en el método del descenso infinito. Es una construcción geométrica clásica de regla y compás, probando el teorema por un modo muy similar a como lo hacían los antiguos geómetras griegos.

Sea ABC un triángulo rectángulo isósceles con hipotenusa de longitud de m y catetos de longitud n. Por el teorema de Pitágoras, n ² + n ² = m ² ; 2n ² =m ² ; $\scriptstyle{\sqrt{2}}$ = m/n.

Supongamos que m y n son números enteros.

Trazamos los arcos BD y CE con centro en A. Unimos DE. Se sigue que AB = AD, AC = AE y el ∠BAC y el ∠DAE coinciden. Por lo tanto los triángulos ABC y ADE son congruentes por tener dos lados iguales y el ángulo comprendido también.

Como ∠EBF es un ángulo recto y ∠BEF es la mitad de un recto, BEF es también un triángulo rectángulo isósceles. Se cumple que BE = BF = m − n. Razonando análogamente, FDC es también un triángulo rectángulo isósceles, con catetos DF = DC = m − n, y con hipotenusa FC = n − (m − n) = 2n − m, que son números también enteros y menores a n y m respectivamente. Al ser ABC y FDC dos triángulos semejantes podemos repetir el anterior proceso de forma recurrente. Con las longitudes de las hipotenusas y con las de los catetos de los sucesivos triángulos, obtenemos dos sucesiones de números enteros estrictamente decrecientes que no son finitas, lo cual es imposible porque si n y m son enteros debe existir una fracción irreducible. Esta contradicción nos hace concluir que la suposición de que m y n son números enteros es falsa y que $\scriptstyle{\sqrt{2}}$ no puede ser una fracción $\textstyle{\frac{m}{n}}$ con m y n enteros, por tanto $\scriptstyle{\sqrt{2}}$ tiene que ser un número irracional.

Prueba basada en argumentos de paridad

Se asume que: $\scriptstyle{\sqrt{2}}$ es un número racional, con ello se sabe que existen dos números enteros a y b tal que se satisfaga que la fracción a / b = $\scriptstyle{\sqrt{2}}$ .
Entonces $\scriptstyle{\sqrt{2}}$ puede ser escrito como una fracción irreducible (la fracción es reducida tanto como sea posible) a / b tal que a y b son números primos entre sí y (a / b)² = 2.
Se sigue que a² / b² = 2 y a² = 2 b².
Por lo tanto a² es par debido a que es igual a 2 b² lo cual es obvio.
Se sigue que a debe ser número par. (Los números impares tienen raíces impares y los pares tienen raíces pares.)
Debido a que a es par, entonces existe un número entero k tal que satisface: a = 2k.
Insertamos la última ecuación de (3) en (6): 2b² = (2k)² es equivalente a 2b² = 4k² es equivalente a b² = 2k².
Debido a que 2k² es par se deduce que b² es también par lo que significa que b es par porque sólo los números pares tienen raíces cuadradas pares.
Como (4) y (8) a y b son ambos pares, lo que contradice que a / b es irreducible tal y como se afirmó en (2).

como se ha encontrado una contradicción al asumir en (1) que $\scriptstyle{\sqrt{2}}$ es un número racional, se deduce que esta afirmación es falsa. Se demuestra entonces lo contrario: $\scriptstyle{\sqrt{2}}$ es irracional.

Prueba más general (y simple)

Supongamos que $\scriptstyle{\sqrt{2}}$ es un número racional. La escribimos en forma de fracción irreducible a/b . Esto significa que a y b son enteros sin factores primos comunes. De donde se deduce que a² y b² tampoco pueden tener factores comunes. Por lo que la fracción a²/b² será también irreducible y tendrá una única expresión que será a²/b² = 2/1, lo que implica a² = 2, lo cual es imposible ya que a es un número entero. La contradicción ha aparecido.

Esta prueba puede ser generalizada para mostrar como cualquier raíz de cualquier número natural es o bien un número natural o un número irracional.

Propiedades de la raíz cuadrada de dos

La mitad de $\sqrt{2}$ , es aproximadamente 0,70710 67811 86548, y es muy usado en geometría y trigonometría, debido, en parte, a que el vector unitario que hace un ángulo de 45° con los ejes de un plano tiene como coordenadas:

$\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right).$

Este número satisface:

$\frac{\sqrt{2}}{2} = \sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} = \cos(45^\circ) = \sin(45^\circ).$

Una propiedad interesante de la raíz cuadrada de dos es la que sigue:

$\!\ {1 \over {\sqrt{2} - 1}} = \sqrt{2} + 1.$

Este resultado es una propiedad de la razón plateada.

La raíz cuadrada es conocida también como una fracción continua

$\!\ 1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \cdots}}}.$

Series y representaciones en productos

La identidad $\cos\left(\frac{\pi}{4}\right) = \sin\left(\frac{\pi}{4}\right) = \frac{1}{\sqrt{2}}$ , mediante un producto infinito de senos y cosenos, queda como sigue

$\frac{1}{\sqrt 2} = \prod_{k=0}^\infty \left(1-\frac{1}{(4k+2)^2}\right) = \left(1-\frac{1}{4}\right) \left(1-\frac{1}{36}\right) \left(1-\frac{1}{100}\right) \cdots$

$\sqrt{2} = \prod_{k=0}^\infty \frac{(4k+2)^2}{(4k+1)(4k+3)} = \left(\frac{2 \cdot 2}{1 \cdot 3}\right) \left(\frac{6 \cdot 6}{5 \cdot 7}\right) \left(\frac{10 \cdot 10}{9 \cdot 11}\right) \left(\frac{14 \cdot 14}{13 \cdot 15}\right) \cdots$

o equivalentemente

$\sqrt{2} = \prod_{k=0}^\infty \left(1+\frac{1}{4k+1}\right) \left(1-\frac{1}{4k+3}\right) = \left(1+\frac{1}{1}\right) \left(1-\frac{1}{3}\right) \left(1+\frac{1}{5}\right) \left(1-\frac{1}{7}\right) \cdots.$

El número puede ser expresado mediante una expansión en serie de Taylor de una función trigonométrica. Por ejemplo, las series para $\cos\left(\frac{\pi}{4}\right)$ da

$\frac{1}{\sqrt{2}} = \sum_{k=0}^\infty \frac{(-1)^k \left(\frac{\pi}{4}\right)^{2k}}{(2k)!}$

La serie de Taylor de: $\sqrt{(1+x)}$ x = 1 proporciona:

$\sqrt{2} = \sum_{k=0}^\infty (-1)^{k+1} \frac{(2k-3)!!}{(2k)!!} = 1 + \frac{1}{2} - \frac{1}{2\cdot4} + \frac{1\cdot3}{2\cdot4\cdot6} - \frac{1\cdot3\cdot5}{2\cdot4\cdot6\cdot8} + \cdots.$

La convergencia de esta serie puede ser acelerada por una transformada de Euler, produciendo

$\sqrt{2} = \sum_{k=0}^\infty \frac{(2k+1)!}{(k!)^2 2^{3k+1}} = \frac{1}{2} +\frac{3}{8} + \frac{15}{64} + \frac{35}{256} + \frac{315}{4096} + \frac{693}{16384} + \cdots.$

No se sabe si $\sqrt{2}$ puede ser representado con una fórmula de tipo BBP. Sin embargo, si se conocen las fórmulas de tipo-BBP para π $\sqrt{2}$ y para $\sqrt{2}$ $\ln(1+\sqrt{2})$ . [1]

Distintas expresiones

Binario: 1.0110101000001001111...

Decimal: 1.4142135623730950488...

Hexadecimal: 1.6A09E667F3BCC908B2F...

Fracción continua: $1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{\ddots}}}}$

Véase también

La raíz cuadrada de dos es el cociente de aspecto del Formato de papeles bajo ISO 216.

Bibliografía

Flannery, David (2005). The Square Root of Two. Springer. ISBN 0-387-20220-X.
Fowler, David; Eleanor Robson (noviembre 1998). «Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context» (PDF). Historia Mathematica 25 (4): pp. 366-378. http://www.hps.cam.ac.uk/dept/robson-fowler-square.pdf.
Gourdon, X. & Sebah, P. Pythagoras' Constant: $\sqrt{2}$ . Incluye información de como calcular dígitos de $\sqrt{2}$ .
Henderson, David W., Square Roots in the Sulbasutra
Weisstein, Eric W. «Pythagoras's Constant» (en inglés). MathWorld. Wolfram Research.

Referencias

↑ Tabla de dígitos de raíz cuadrada de dos.
↑ Fowler and Robson, p. 368.
Fotografía, ilustración, y descripción de la root(2) tablilla procedente de la "Yale Babylonian Collection"
Fotografías de alta resolución y análisis descriptivo de las tablas de la root(2) (YBC 7289) procedente de la "Y"ale Babylonian Collection"
↑ Henderson.
↑ Aunque se denomine "Método babilónico" generalmente, no existe evidencia que muestre un uso de esta aproximación por los babilónicos en el cálculo de la aproximación de $\sqrt{2}$ tal y como se puede ver en la tablilla YBC 7289. Fowler and Robson ofrece generalmente detalle y conjeturas sobre esto.
Fowler and Robson, p. 376. Flannery, p. 32, 158.
↑ Number of known digits

Enlaces externos

La raíz cuadrada de 2 con cinco millones de dígitos por Bonnell & Robert Nemiroff. May, 1994.
Bogomolny, Alexander. «Square root of 2 is irrational» (en inglés). Interactive Mathematics Miscellany and Puzzles., una colección de pruebas
√2.net, sítio de entusiastas del número con cálculos on-line

Categorías:

Constantes matemáticas
Raíces
Números irracionales

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

Raíz cuadrada de 5 — Saltar a navegación, búsqueda La raíz cuadrada de 5 es el número real positivo que, cuando es multiplicado por si mismo, da el número primo 5. Este número es notable en parte porque aparece en la fórmula para el número áureo. Puede ser denotado… … Wikipedia Español
Raíz cuadrada — Expresión matemática de raíz cuadrada de X . La … Wikipedia Español
Raíz cuadrada de 3 — La raíz cuadrada de 3 es igual a la longitud a través de los lados planos de un hexágono regular con los lados de la longitud 1. La raíz cuadrada de tres es un número real positivo que cuando es multiplicado por sí mismo da el número tres. Se… … Wikipedia Español
Raíz cuadrada — ► locución MATEMÁTICAS Cantidad que se ha de multiplicar por sí misma una vez para obtener un número determinado. * * * En matemáticas, la raíz cuadrada de un número real no negativo x es el número real no negativo que, multiplicado con sí mismo … Enciclopedia Universal
Raíz cuadrada negativa — Saltar a navegación, búsqueda La raíz cuadrada principal de un número negativo real, se denota de la siguiente manera √ a donde a es positiva, y esta definida por: √ a = i√a donde i es la unidad imaginaria i=√ 1 ejemplos: a) √ 4 = i√4 = 2i b) 4+√ … Wikipedia Español
Cálculo de la raíz cuadrada — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar … Wikipedia Español
Raíz enésima de un número — Saltar a navegación, búsqueda La raíz enésima de un número a es igual a b , es decir Contenido 1 Partes de la raíz enésima 2 Casos de raíz enésima … Wikipedia Español
raíz — sustantivo femenino 1. Área: botánica Parte de las plantas que crece en sentido contrario al tallo y por la cual la planta se fija al suelo y absorbe los alimentos que necesita: Este árbol tiene las raíces muy profundas. 2. Parte de una cosa por… … Diccionario Salamanca de la Lengua Española
Raíz — Saltar a navegación, búsqueda La palabra raíz tiene varios significados, todos derivados del término botánico que han sido adoptados en otras áreas del conocimiento: Botánica Raíz: órgano subterráneo de las plantas que absorbe el agua y los… … Wikipedia Español
raíz — (Del lat. radix, ĭcis). 1. f. Bot. Órgano de las plantas que crece en dirección inversa a la del tallo, carece de hojas e, introducido en tierra o en otros cuerpos, absorbe de estos o de aquella las materias necesarias para el crecimiento y… … Diccionario de la lengua española

Los diccionarios y las enciclopedias sobre el Académico

Raíz cuadrada de 2

Contenido

Historia

Algoritmo computacional