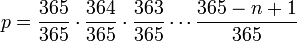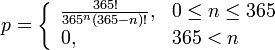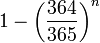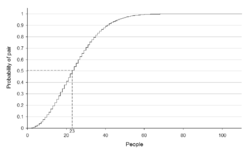
La paradoja del cumpleaños establece que si hay 23 personas reunidas, hay una probabilidad del 50,7% de que al menos dos personas de ellas cumplan años el mismo día. Para 60 o más personas la probabilidad es mayor del 99%. Obviamente es del 100% para 367 personas (teniendo en cuenta los años bisiestos). En sentido estricto esto no es una paradoja ya que no es una contradicción lógica; es una paradoja en el sentido que es una verdad matemática que contradice la común intuición. Mucha gente piensa que la probabilidad es mucho más baja, y que hacen falta muchas más personas para que se alcance la probabilidad del 50%.

Estimación de la probabilidad

Calcular esta probabilidad es el problema del cumpleaños. La teoría fue descrita en American Mathematical Monthly en 1938 en la teoría de Estimación del total de población de peces en un lago de Zoe Emily Schnabel, bajo el nombre de captura-recaptura estadística.

La clave para entender la paradoja del cumpleaños es pensar que hay muchas probabilidades de encontrar parejas que cumplan años el mismo día. Específicamente, entre 23 personas, hay 23×22/2 = 253 pares, cada uno de ellos un candidato potencial para cumplir la paradoja. Hay que entender que si una persona entrase en una habitación con 22 personas, la probabilidad de que cualquiera cumpla años el mismo día que quien entra, no es del 50%, es mucho más baja. Esto es debido a que ahora sólo hay 22 pares posibles. El problema real de la paradoja del cumpleaños consiste en preguntar si el cumpleaños de cualquiera de las 23 personas coincide con el cumpleaños de alguna de las otras personas.

Calculemos la probabilidad aproximada de que en una habitación de n personas, que al menos dos cumplan años el mismo día, desechando los años bisiestos y las personas gemelas, y asumimos que existen 365 cumpleaños que tienen la misma probabilidad. El truco es calcular primero la probabilidad de que n cumpleaños sean diferentes. Esta probabilidad es dada por

porque la segunda persona no puede tener el mismo cumpleaños que el primero (364/365), la tercera personas no puede tener el mismo cumpleaños que las dos primeras (363/365), etc. Usando notación factorial, puede ser escrita como

Ahora, 1 - p es la probabilidad que al menos dos personas tengan el mismo día de cumpleaños. Para n = 23 se obtiene una probabilidad de alrededor de 0,507.

En contraste, la probabilidad que cualquiera en una habitación de n personas tengan el mismo día de cumpleaños que usted está dada por

que para n = 22 sólo da alrededor de 0,059, y se necesitaría al menos una n de 253 para dar un valor de 0,5.

Programa en Pascal que calcula las probabilidades desde 1 hasta 100

Program Cumples ;
Var
   i : Integer ;
   p : Real ;
Begin
   Writeln(' Num. Probabilidad') ;
   p := 1.0 ;
   For i := 1 to 100 Do
   Begin
      p := p * (366 - i) / 365 ;
      Write(i:3,' : ',1-p:10:6) ;
      Readln ;
   End ;
End.

Programa en Python que calcula las probabilidades desde 1 hasta 100

print 'Num. probabilidad'
p = 1.0
for i in xrange(1, 100):
    p = p * (366 - i) / 365
    print '%3d : %10.6f' % (i, p)

Enlaces externos

• Simulación de la Paradoja del Cumpleaños. Inspección de 50 habitaciones, con diferente cantidad de personas, desde 1 hasta 101.