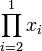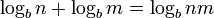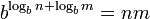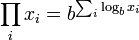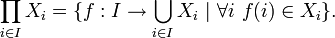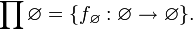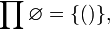Producto vacío

Producto vacío

Producto vacío

En matemáticas, un producto vacío es el resultado de multiplicar entre sí ningún número. Su valor numérico es 1, el elemento neutro del producto, de la misma manera que la suma vacía, que es el resultado de sumar entre sí ningún número, vale cero, el elemento neutro de la suma.[1] [2] [3]

El producto vacío se utiliza en matemáticas discretas, álgebra, el estudio de series de potencias y en la programación.

Contenido

Producto aritmético de cero factores

Ejemplos

Dos ejemplos frecuentes de producto vacío son a0 = 1 (cualquier número elevado a la potencia cero vale uno) y 0! = 1 (el factorial de cero vale uno).

También se puede hablar de producto vacío en el caso en que el índice inferior de un productorio es mayor que el índice superior, por ejemplo,

\prod_{i=2}^1 x_i

Como no existe ningún índice que satisfaga ambas condiciones, es decir, el intervalo [2,1] es vacío, el productorio no consta de ningún factor y por tanto vale uno.

Se pueden encontrar más ejemplos de producto vacío en los siguientes artículos: demostración de que e es irracional, factorial, factor primo, número de Stirling, operador diferencia, paradoja del cumpleaños, símbolo de Pochhammer, teorema binomial, teorema de König, teorema fundamental de la aritmética.

Justificación intuitiva

Imagine una calculadora que sólo puede multiplicar. Dispone, además de los botones correspondientes a las cifras del 0 al 9, de otros dos botones: "INTRO" y "BORRAR". Se pretende que, si introduce la secuencia "BORRAR - 7 - INTRO - 3 - INTRO - 4 - INTRO", el resultado leído en pantalla sea "84", porque 7×3×4=84. En general, se pretende que:

  • la calculadora muestre un número justo después de que el usuario pulse la tecla "BORRAR".
  • si hay un número en pantalla y el usuario introduce otro número, se muestre el producto.
  • cuando se pulse la tecla "BORRAR" y después se introduzca una secuencia de números, la calculadora muestre su producto.

Entonces, el valor inicial tras pulsar la tecla "BORRAR" debe ser "1". Por tanto, el producto de cero factores vale 1.

Logaritmos

La definición de un producto vacío se puede derivar de la de la suma vacía:

La suma de dos logaritmos es igual al logaritmo del producto de sus operandos, es decir, para cualquier base b>0 se tiene:

\log_b n + \log_b m = \log_b nm\,

y

b^{\log_b n + \log_b m} = nm

y de forma más general

\prod_i x_i = b^{\sum_i \log_b x_i}

es decir, que el producto de todos los elementos de un conjunto es b elevado a la suma de los logaritmos de los elementos de ese conjunto.

Usando esta propiedad como definición y extendiéndola al producto vacío, el miembro derecho de esta ecuación vale b0 para el conjunto vacío, porque la suma vacía vale 0 por definición, y por tanto el producto vacío debe valer 1.

00

En teoría de conjuntos y combinatoria, el número cardinal nm es el tamaño del conjunto de funciones que va de un conjunto de tamaño m a un conjunto de tamaño n. Si m es positivo y n es cero, entonces no hay tales funciones porque no existen elementos del segundo conjunto que correspondan a elementos del primer conjunto. Entonces, 0m = 0 cuando m es positivo. Sin embargo, si los dos conjuntos son vacíos (su cardinal es 0), entonces hay una única función, la función vacía, que cumple la condición. Por este motivo, en estos campos de la matemática es frecuente definir 00 como 1 cuando representa un producto vacío.

Intersección nularia

Por motivos similares, la intersección de un conjunto vacío de subconjuntos de un conjunto X es por convención igual a X.

Producto cartesiano nulario

Considérese la definición general del producto cartesiano:

\prod_{i \in I} X_i = \{ f : I \to \bigcup_{i \in I} X_i\ |\ \forall i\ f(i) \in X_i \}.

Si I es vacío, la única f que satisface la condición es la función vacía:

\prod \varnothing = \{ f_\varnothing: \varnothing \to \varnothing \}.

Por tanto, el cardinal del producto cartesiano de ningún conjunto es 1.

Según la interpretación más típica en n-uplas,

\prod \varnothing = \{ ( ) \},

es decir, el conjunto unitario que contiene únicamente la dupla vacía. Nótese que en ambas representaciones el producto vacío tiene cardinal 1.

Referencias

  1. ↑ Jaroslav Nešetřil, Jiří Matoušek (1998). Invitation to Discrete Mathematics. Oxford University Press, pp. 12. ISBN 0-19-850207-9.
  2. ↑ A.E. Ingham and R C Vaughan (1990). The Distribution of Prime Numbers. Cambridge University Press, pp. 1. ISBN 0-521-39789-8.
  3. ↑ Serge Lang (2002). Algebra. Springer-Verlag, pp. 9. ISBN 0-387-95385-X.
Obtenido de "Producto vac%C3%ADo"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Producto cartesiano — Saltar a navegación, búsqueda En teoría de conjuntos, el producto cartesiano es un producto directo de conjuntos. En particular, el producto cartesiano de dos conjuntos X y Y, denotado por X × Y, es el conjunto de todos los pares ordenados en los …   Wikipedia Español

  • Producto sanitario para diagnóstico in vitro — Saltar a navegación, búsqueda Un producto sanitario para diagnóstico in vitro es, según la directiva europea 98/79/EC: cualquier producto sanitario que consista en un reactivo, producto reactivo, calibrador, material de control, estuche de… …   Wikipedia Español

  • Vacío — (Del lat. vulgar vacivus.) ► adjetivo 1 Que no tiene contenido o no tiene algo determinado: ■ botella de vino vacía. ANTÓNIMO lleno 2 Que no está ocupado por nadie o que está sin gente o con poca gente: ■ la ciudad estaba vacía; el cine está… …   Enciclopedia Universal

  • Conjunto vacío — El conjunto vacío es aquél que no tiene elementos. En matemáticas, específicamente en teoría de conjuntos, el conjunto vacío es el conjunto que no contiene ningún elemento. Puesto que lo único que define a un conjunto son sus elementos, el… …   Wikipedia Español

  • Filtración a vacío — Saltar a navegación, búsqueda La Filtración al vacio es un método fisico que se utiliza para separar mezclas heterogéneas: un producto sólido de un solvente o mezcla de reacción líquida. La mezcla se vierte en un embudo a través de un papel… …   Wikipedia Español

  • Suma vacía — En matemática, una suma vacía es una sumatoria en la que no interviene ningún término. El valor de una suma vacía de números es por convención igual a cero. Para sumatorias entre entidades no numéricas (vectores, matrices, polinomios, etc.)… …   Wikipedia Español

  • Teorema fundamental de la aritmética — En matemática, y particularmente en la teoría de números, el teorema fundamental de la Aritmética o teorema de factorización única afirma que todo entero positivo se puede representar de forma única como producto de factores primos. Por ejemplo,… …   Wikipedia Español

  • Número primo — Un número primo es un número natural mayor que 1, que tiene únicamente dos divisores distintos: él mismo y el 1. Se contraponen así a los números compuestos, que son aquellos que tienen algún divisor natural aparte de sí mismos y del 1. El número …   Wikipedia Español

  • Factorial — ► sustantivo femenino MATEMÁTICAS Producto de la multiplicación de todos los términos de una progresión aritmética. * * * factorial (de «factor») 1 f. Mat. Producto de todos los términos de una progresión aritmética. 2 m. Mat. Producto de todos… …   Enciclopedia Universal

  • Conjunto generador de un grupo — En teoría de grupos, un conjunto generador de un grupo G es un subconjunto S de G tal que todo elemento de G puede ser expresado como el producto de un número finito de elementos de S y de sus inversos. Más generalmente, si S ⊆ G, <S> es el …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”