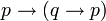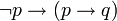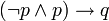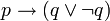Las paradojas de la implicación material son un conjunto de fórmulas de la lógica proposicional, reconocidas como verdades lógicas, pero que golpean al sentido común como cuestionables, o incluso absurdas.^[1] Algunas de estas son:

• 
• 
• 
• 

Dicho en términos más concretos, la lógica proposicional afirma que las siguientes oraciones son verdaderas:

• Si la Luna está hecha de queso, entonces 2 + 2 = 4.
• Si 2 + 2 = 5, entonces la Luna está hecha de queso.
• Si la Luna está hecha de queso, entonces la Tierra es plana o no es plana.

Como la verdad de estas oraciones resulta tan anti-intuitiva, muchos filósofos han afirmado que se comete un error al considerarlas verdades lógicas. En general se piensa que dicho error reside en la interpretación veritativo-funcional del condicional «si..., entonces...», y por lo tanto se han propuesto varias alternativas, entre ellas el condicional estricto, y los esfuerzos de la lógica relevante.

En el lenguaje cotidiano, la expresión "si..., entonces..." puede denotar una relación causal, pero esto no es así según la lógica proposicional. De manera que la expresión: "si Manhattan está en Siberia, entonces el presidente Bush es un mono", aunque parezca absurda, lógicamente es verdadera. Según algunos críticos, muchos de los problemas de la filosofía de la ciencia han ocurrido por el uso del condicional "si-entonces" en vez de "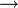" como noción de implicación. Por otra parte, la noción de "implicación" denotada por 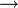ha llevado a grandes descubrimientos en lógica y matemática.^[2]

El problema es que el uso veritativo-funcional del condicional, tal y como se hace en lógica, no da cuenta del uso que en el lenguaje ordinario hacemos de la implicación, pues la interpretación del condicional nos dice que si el antecedente es falso, el valor del condicional es verdadero. O que si antecedente y consecuente son falsos, el valor del condicional es verdadero.

Todo esto responde a que en la lógica, el sentido de las tablas de verdad es tomar en cuenta todos los posibles estados del mundo. Por ejemplo, en la proposición "llueve y hace calor" los estados posibles del mundo son cuatro: que llueva y haga calor, que llueva y no haga calor, que no llueva y haga calor, o que ni llueva ni haga calor.

De manera, que el valor del condicional se rige, en el lenguaje lógico, por estructuras lógicas que no se relacionan necesariamente con la realidad, sino que parten de lo que podría pasar en el mundo al cual se refiere la preposición.

Por eso, en lógica son válidos esquemas como los que se citan a continuación, que son ejemplos de las llamadas paradojas del condicional material:

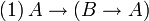
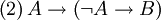
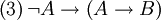
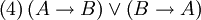
Para ejemplificar lo que ocurre, consideremos las proposiciones (1) y (2).

Lo que (1) dice es que una proposición verdadera será implicada por cualquier proposición. Es decir, si A es verdadera, B (otra proposición cualquiera), implica A.

Con respecto a (2), lo que dice es que la negación de una proposición verdadera implicará cualquier otra. Es decir, si A (es verdadera), entonces la negación de A implica B (otra proposición).

Ahora bien, qué pasaría si sustiyéramos "A" por "2+2=4" y "B" por "la luna es verde". Teniendo en cuenta que "2+2=4" es verdadero, de (1) y (2), podemos obtener inferencias como las siguientes:

(3) Si la luna es verde, entonces 2+2=4.

(4) Si 2+2 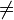4, entonces la luna es verde.

Tanto (3) como (4) entran en conflicto con la idea de implicación que se da en el discurso ordinario, y son ejemplos paradigmáticos de estas paradojas. Por esta razón, se ha dicho que el condicional clásico es paradójico y, en consecuencia, también lo es la propia lógica clásica.

En un artículo en 1961 Rolf Eberle, David Kaplan y Richard Montague explotan las célebres paradojas de la implicación material para demostrar que, a grandes rasgos, por lo mismo que se explica un hecho cualquiera se puede explicar cualquier otro hecho (entrando en debate con Hempel y Oppenheim que afirmaban un modelo nomológico- deductivo para la explicación científica). En el mismo número de esa revista David Kaplan en un célebre artículo publicó una solución satisfactoria del problema, que podía ser resuelto por una serie de argucias técnicas.

Véase también

• Implicación
• Paradojas de la implicación estricta
• Lógica relevante
• Tabla de valores de verdad

Enlaces externos

Peter Suber: Paradoxes of Material Implication

Notas y referencias