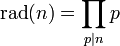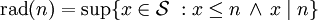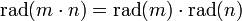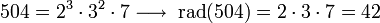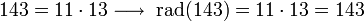Radical de un entero

Radical de un entero

Radical de un entero

En teoría de números, el radical de un entero positivo n, es el producto de los números primos que dividen n. Se utiliza en diversas partes de la teoría de números, por ejemplo, en la formulación de la conjetura abc. Suele llamarse también parte libre de cuadrados de n ( en inglés square-free part of n ).

Contenido

Definición

La definición formal es la siguiente:

Si

n = p_1^{\alpha_1} \cdots p_k^{\alpha_k} \quad \quad \alpha_k \in \mathbb{N}_0,\;p \in \mathbb{P}

es un número natural formado por factores primos distintos elevados a un cierto exponente, entonces:

\operatorname{rad} (n) = \prod_{p \mid n} p

Otra definición equivalente, considerando 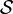\mathcal{S} el conjunto de enteros positivos que son libres de cuadrados, es:

\operatorname{rad} (n) = \sup \{ x \in \mathcal{S} \; : x \leq n \, \land \, x \mid n \}

o sea, el mayor entero libre de cuadrados que divide a n. Por convenio, rad(1) = 1.

Los radicales de los primeros números enteros positivos son 1, 2, 3, 2, 5, 6, 7, 2, 3, 10,... (secuencia A007947 en OEIS)

Propiedades

\operatorname{rad}(m \cdot n) = \operatorname{rad}(m) \cdot \operatorname{rad}(n)

Ejemplos

Algunos ejemplos:

504=2^3\cdot3^2\cdot7 \longrightarrow \; \mbox{rad}(504)=2\cdot3\cdot7=42
143 = 11 \cdot 13 \longrightarrow \; \mbox{rad}(143) = 11 \cdot 13 = 143

Enlaces externos

Obtenido de "Radical de un entero"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Radical — Saltar a navegación, búsqueda El término radical viene del latín radix ( raíz ), significa así de raíz o de base, refiriéndose sobre todo a un punto de vista profundo, sustancial, más aún si es aplicado a alguna convicción, práctica, análisis o… …   Wikipedia Español

  • Radical de un ideal — Saltar a navegación, búsqueda En teoría de anillos, una rama de las matemáticas, el radical de un anillo nos muestra ciertas propiedades malas del anillo. Hay diferentes tipos de radicales, como el nilradical o el radical de Jacobson, así como… …   Wikipedia Español

  • Radical jerarquizado — Saltar a navegación, búsqueda En álgebra los radicales jerarquizados son las expresiones radicales que contienen en su interior otra expresión radical. Como en estos ejemplos: Resolver estos radicales se considera generalmente un problema difícil …   Wikipedia Español

  • Historia de la Unión Cívica Radical: 1916-1930 — Saltar a navegación, búsqueda Hipólito Yrigoyen …   Wikipedia Español

  • Historia de la Unión Cívica Radical (1916-1930) — Hipólito Yrigoyen. Marcelo T. de Alvear. En 1916 s …   Wikipedia Español

  • Trimeresurus —   Trimeresurus …   Wikipedia Español

  • Raíz cuadrada — Expresión matemática de raíz cuadrada de X . La …   Wikipedia Español

  • Edad Contemporánea — La carga de los mamelucos, de Francisco de Goya, 1814, representa un episodio del levantamiento del 2 de mayo de 1808 en Madrid. Los pueblos europeos, convertidos en protagonistas de su propia historia y a los que se les había proclamado sujetos… …   Wikipedia Español

  • Historia contemporánea de España — La promulgación de la Constitución de 1812, obra de Salvador Viniegra (Museo de las Cortes de Cádiz). Historia contemporánea de España es la disciplina historiográfica y el periodo histórico de la historia de España que corresponde a la Edad… …   Wikipedia Español

  • Yihadismo — Para el concepto original islámico, véase Yihad. Atentado contra las Torres Gemelas.[1] El yihadismo es un …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”