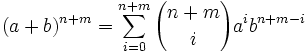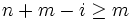Radical de un ideal

Radical de un ideal

Radical de un ideal

En teoría de anillos, una rama de las matemáticas, el radical de un anillo nos muestra ciertas propiedades malas del anillo. Hay diferentes tipos de radicales, como el nilradical o el radical de Jacobson, así como una teoría de propiedades generales radicales.

Definición de radical de un ideal.

Sea R un Anillo conmutativo y sea I un ideal del anillo. El conjunto 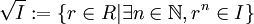\sqrt{I}:= \{r \in R | \exist n \in \mathbb{N}, r^n \in I\} (también denotado por Rad(I)) se denomina radical del ideal I (o sencillamente radical de I).

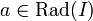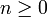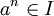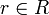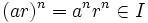Si a \in \hbox{Rad}(I) es que existe un entero n \geq 0 tal que a^n \in I. Así, si r \in R es (a r)^n = a^n r^n \in I.

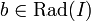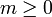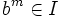Si además b \in \hbox{Rad}(I) existirá otro entero m \geq 0 de manera que b^m \in I.

Por el Teorema del binomio:

(a+b)^{n+m}=\sum_{i=0}^{n+m}{n+m\choose i}a^ib^{n+m-i}
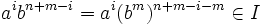  • Si i < n entonces es n + m − i > n + m − n = m, luego el exponente de b es mayor o igual que m, y así a^i b^{n+m-i}=a^i (b^m)^{n+m-i-m} \in I.
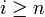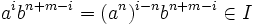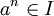  • Si i \geq n entonces es a^i b^{n+m-i} = (a^n)^{i-n} b^{n+m-i} \in I ya que a^n \in I.

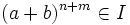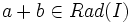En cualquier caso, cada sumando de (a + b)n + m está en I, que es un ideal de R, luego (a+b)^{n+m} \in I y será a+b \in Rad(I).

Así Rad(I) es un ideal de R.

Un ideal I de un anillo conmutativo y unitario R se dice que es ideal radical si coincide con su radical, esto es, si Rad(I) = I. Como es obvio, el radical de un ideal es siempre un ideal radical.

Todo ideal primo es radical: En efecto, Si P es un ideal primo, entonces R / P es un dominio íntegral, esto es, no tiene divisores de cero, y en particular no puede tener nilpotentes.

Es sencillo comprobar que si tomamos \pi:R \longrightarrow R/I la proyección canónica de R sobre I, entonces Rad(I) = π − 1(N(R / I)) (de hecho mediante esta demostración se demuestra de manera inmediata que Rad(I) es un ideal de R; aquí, N(R) es el nilradical de R, definido más abajo). Para ver esto, notar en primer lugar que si 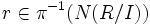r \in \pi^{-1}(N(R/I)), entonces para algún 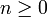n \geq 0, π(r)n = π(rn) es cero en R / I, y por tanto rn está en I. 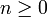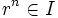Recíprocamente, si rn está en I para algún n \geq 0 será r^n \in I, entonces (π(r))n = π(rn)es cero en R / I, y por tanto π(r) está en N(R / I).


Mediante el uso de la localización, podemos ver que Rad(I) es la intersección de todos los ideales primos de R que contienen a I: cada ideal primo es radical, así que la intersección de los ideales primos que contienen a I contienen a Rad(I). Si r es un elemento de R que no está en Rad(I), entonces sea S el conjunto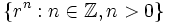 \{r^n: n \in \mathbb{Z}, n > 0 \}. S es multiplicativamente cerrado, así que podremos formar la localización S − 1R.

El nilradical.

Sea R un Anillo conmutativo. Primero mostraremos que los elementos nilpotentes de R forman un ideal N. Sean a y b elementos nilpotentes de R con an = 0 y bm = 0. Probamos que a + b es nilpotente. Podemos usar el Teorema del binomio para expandir (a+b)^(n+m) :

(a+b)^{n+m}=\sum_{i=0}^{n+m}{n+m\choose i}a^ib^{n+m-i}

Para cada i, se da una y sólo una de las siguientes condiciones:

  • i \geq n
  • n+m-i \geq m

Esto dice que en cada expresión 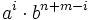a^i \cdot b^{n+m-i}, o bien el exponente de a será lo suficientemente grande como para anular la expresión (si i < n entonces es n + m − i > n + m − n = m, luego el exponente de b es mayor o igual que m, y así 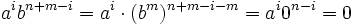a^i b^{n+m-i}=a^i \cdot(b^m)^{n+m-i-m}=a^i 0^{n-i}=0), o bien el exponente de b será lo suficientemente grande como para anular la expresión (si 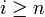i \geq n entonces es aibn + m − i = (an)i − nbn + m − i = 0i − nbn + m − i = 0). Así tenemos que a + b es nilpotente, y por tanto está en N.

Para terminar de comprobar que N es un ideal, cogemos un elemento arbitrario 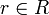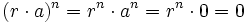r \in R. (r \cdot a)^n = r^n \cdot a^n = r^n \cdot 0 = 0, así que 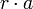r \cdot a es nilpotente, y está por tanto en N. Con lo que N es un ideal.

N se denomina entonces nilradical de R, o radical nilpotente de R, y se denota por N(R). Al anillo 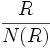\frac{R}{N(R)} se le denomina anillo reducido (asociado a R), aunque esta denominación está cayendo en el desuso.

Es inmediato comprobar que N(R / N(R)) = {0}.

Es sencillo demostrar que N(R) = Rad({0}), esto es, que el nilradical de un anillo es precisamente el radical del ideal nulo. Por esto, el nilradical de R es la intersección de todos los ideales primos de R.

Obtenido de "Radical de un ideal"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Radical D'un Idéal — Soit A un anneau commutatif. Soit I un idéal de A. Le radical de I est l ensemble . C est un idéal de A, propre si I est propre, contenant I. Si I = {0} on parle de nilradical. Si I est un idéal propre de A son radical est l intersection des… …   Wikipédia en Français

  • Radical d'un ideal — Radical d un idéal Soit A un anneau commutatif. Soit I un idéal de A. Le radical de I est l ensemble . C est un idéal de A, propre si I est propre, contenant I. Si I = {0} on parle de nilradical. Si I est un idéal propre de A son radical est l… …   Wikipédia en Français

  • Radical of an ideal — In ring theory, a branch of mathematics, the radical of an ideal is a kind of completion of the ideal. There are several special radicals associated with the entire ring such as the nilradical and the Jacobson radical , which isolate certain bad… …   Wikipedia

  • Radical d'un idéal — Pour les articles homonymes, voir Radical. En algèbre commutative, le radical d un idéal I dans un anneau commutatif A est l ensemble des éléments de A dont une puissance appartient à I. Sommaire 1 Définition 2 …   Wikipédia en Français

  • Radical de un ideal — En teoría de anillos, una rama de las matemáticas, el radical de un anillo nos muestra ciertas propiedades malas del anillo. Hay diferentes tipos de radicales, como el nilradical o el radical de Jacobson, así como una teoría de propiedades… …   Enciclopedia Universal

  • Radical — Saltar a navegación, búsqueda El término radical viene del latín radix ( raíz ), significa así de raíz o de base, refiriéndose sobre todo a un punto de vista profundo, sustancial, más aún si es aplicado a alguna convicción, práctica, análisis o… …   Wikipedia Español

  • Radical — (from Latin radicis , genitive of radix root ) can refer to many different things and concepts.Mathematics*The symbol √ used to indicate the square root or nth root *Radical of an algebraic group, a concept in algebraic group theory *Radical of… …   Wikipedia

  • Idéal — Pour les articles homonymes, voir Idéal (homonymie). En mathématiques, et plus particulièrement en algèbre, un idéal est un sous ensemble remarquable d un anneau. Par certains égards, les idéaux s apparentent aux sous espaces vectoriels ce sont… …   Wikipédia en Français

  • Idéal premier — Richard Dedekind 1831 1916 formalisateur du concept d idéal En algèbre commutative, un idéal premier d un anneau commutatif unitaire est un idéal tel que le quotient de l anneau par cet idéal est un anneau intègre. Ce concept généralise la notion …   Wikipédia en Français

  • Ideal (teoría de anillos) — En matemáticas, un ideal es una estructura algebraica definida en un anillo. Los ideales generalizan de manera fecunda el estudio de la divisibilidad en los números enteros. De este modo, es posible enunciar versiones muy generales de teoremas… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”