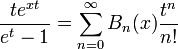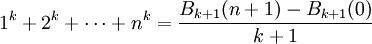Polinomios de Bernoulli

Polinomios de Bernoulli

Polinomios de Bernoulli

En matemáticas, los polinomios de Bernoulli Bn(x) se definen mediante la función generatriz:

\frac{t e^{xt}}{e^t-1}= \sum_{n=0}^\infty B_n(x) \frac{t^n}{n!}

Aparecen en el estudio de numerosas funciones especiales, en particular de la función zeta de Riemann y de la función zeta de Hurwitz. Los números de Bernoulli Bn son los términos independientes de los polinomios correspondientes, i.e., Bn = Bn(0).

La identidad Bk + 1(x + 1) − Bk + 1(x) = (k + 1)xk nos permite dar una forma cerrada de la suma

1^k+2^k+ \cdots + n^k= \frac{B_{k+1}(n+1)-B_{k+1}(0)}{k+1}

Expresión explícita de polinomios de menor grado

B_0(x)=1\,
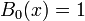
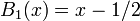
B_1(x)=x-1/2\,
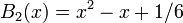
B_2(x)=x^2-x+1/6\,
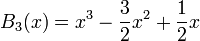
B_3(x)=x^3-\frac{3}{2}x^2+\frac{1}{2}x\,
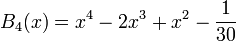
B_4(x)=x^4-2x^3+x^2-\frac{1}{30}\,
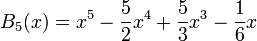
B_5(x)=x^5-\frac{5}{2}x^4+\frac{5}{3}x^3-\frac{1}{6}x\,
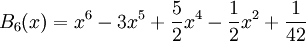B_6(x)=x^6-3x^5+\frac{5}{2}x^4-\frac{1}{2}x^2+\frac{1}{42}\, .

Véase también

Referencias

  • Zwillinger, D. CRC Standard Mathematical Tables and Formulae, CRC Press, 2003. ISBN 1584882913.
Obtenido de "Polinomios de Bernoulli"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Número de Bernoulli — En matemáticas, los números de Bernoulli (denotados por Bn y, a veces, por bn con el fin de distinguirlos de los números de Bell) constituyen una sucesión de números racionales con profundas conexiones en teoría de números. Fueron llamados así… …   Wikipedia Español

  • Número de Bernoulli — Los números de Bernoulli (denotados por y, a veces, por para distinguirlos de los números de Bell ) son números enteros que se obtienen a partir de una forma cerrada de la siguiente expresión para cada valor de . Las formas cerradas de la… …   Enciclopedia Universal

  • Jakob Bernoulli — Jakob Bernoulli. Nacimiento 27 de diciembre de 1654 …   Wikipedia Español

  • Fórmula de Euler-Maclaurin — En matemáticas, la fórmula de Euler Maclaurin relaciona a integrales con series. Esta fórmula puede ser usada para aproximar integrales por sumas finitas o, de forma inversa, para evaluar series (finitas o infnitas) resolviendo integrales. La… …   Wikipedia Español

  • Fórmula de Faulhaber — En Matemáticas, la fórmula de Faulhaber, en honor de Johann Faulhaber, expresa la suma de las potencias de los primeros n números naturales como un polinomio en n de grado (p + 1) cuyos coeficientes se construyen a partir de los números de… …   Wikipedia Español

  • Función polilogarítmica — El polilogaritmo (también conocido como función de Jonquière) es una función especial definida por la siguiente serie: Esta no es, en general, una función elemental, aunque esté relacionada con la función logarítmica. La definición dada arriba es …   Wikipedia Español

  • Números de Stirling de segunda especie — En matemáticas, los Números de Stirling de segunda especie, junto con los Números de Stirling de primera especie, son uno de los dos tipos de Números de Stirling. Comúnmente aparecen en el estudio de la combinatoria, en la que se cuenta el número …   Wikipedia Español

  • Historia de las ecuaciones diferenciales — Una ecuación es una igualdad condicional que se cumple sólo para las soluciones de la misma. Así, en una ecuación algebraica como x – 2 = 0, la igualdad sólo se cumple para x = 2. En forma similar, una ecuación diferencial, constituida por… …   Wikipedia Español

  • Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención …   Wikipedia Español

  • Teorema fundamental del álgebra — El teorema fundamental del álgebra establece que un polinomio en una variable, no constante y con coeficientes complejos, tiene tantas raíces[1] como indica su grado, contando las raíces con sus multiplicidades. En otras palabras, dado un… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”