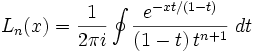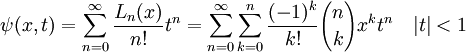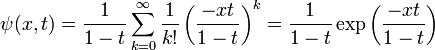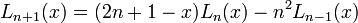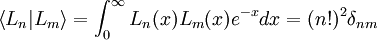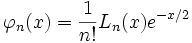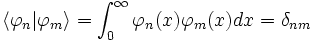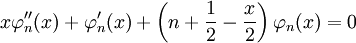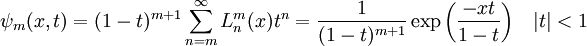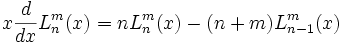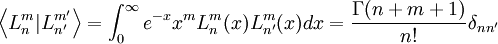Polinomios de Laguerre

Saltar a navegación, búsqueda

Los polinomios de Laguerre son una familia de polinomios ortogonales, llamados así en honor de Edmond Laguerre, surgen al examinar las soluciones a la ecuación diferencial:

$x\,y'' + (1 - x)\,y' + n\,y = 0\,$

Desarrollando $y$ en serie de potencias se obtiene una relación de recurrencia entre coeficientes consecutivos como la que sigue:

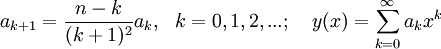
$a_{k+1} = \frac{n-k}{(k+1)^2}a_k,\ \ k=0,1,2,...; \ \ \ y(x) = \sum_{k=0}^\infty a_k x^k\,$

Puede verse que siempre que n sea natural se anula el coeficiente de toda potencia mayor (y distinta) que n. Esto es, una de las soluciones linealmente independientes es un polinomio de grado n (polinomio de laguerre de orden n, que notaremos por L_n(x)). Para encontrar la otra solución linealmente independiente han de estudiarse las soluciones de la ecuación más general $y''(x) + p (x) y'(x) + q (x) y (x) = 0$ .

Contenido

1 Definición
2 Función generatriz
- 2.1 Relaciones de recurrencia
3 Ortogonalidad
4 Polinomios asociados de Laguerre
5 Véase también
6 Referencia

Definición

El polinomio de Laguerre de orden n puede definirse como sigue:

$L_n(x) = (1/(n!))e^x \frac{d^n}{dx^n}(x^ne^{-x})$

Que tras desarrollar queda de la forma:

$L_n(x) = \sum_{k=0}^n (-1)^n {n \choose k} \frac{n!}{k!} x^k = \sum_{k=0}^n (-1)^k \frac{n!n!}{(n-k)!k!k!} x^k$

algunos de estos polinomios son:

n	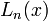$L_n(x)\,$
0	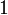$1\,$
1	$-x+1\,$
2	$(1/2)(x^2-4x+2) \,$
3	$(1/6)(-x^3+9x^2-18x+6) \,$
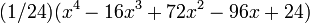
4	$(1/24)(x^4-16x^3+72x^2-96x+24) \,$
5	$(1/120)(-x^5+25x^4-200x^3+600x^2-600x+120) \,$
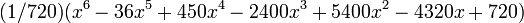
6	$(1/720)(x^6-36x^5+450x^4-2400x^3+5400x^2-4320x+720) \,$

Los polinomios de Laguerre también pueden ser definidos mediante la integral:

$L_n(x)=\frac{1}{2\pi i}\oint\frac{e^{-xt/(1-t)}}{(1-t)\,t^{n+1}} \; dt$

Integrando en sentido contrario a las agujas del reloj sobre cualquier camino cerrado en torno al origen del plano complejo y contenido en el disco |t| < 1.

Función generatriz

La función generatriz de los polinomios de Laguerre viene dada por:

$\psi(x,t) = \sum_{n=0}^\infty \frac{L_n(x)}{n!} t^n = \sum_{n=0}^\infty \sum_{k=0}^n \frac{(-1)^k}{k!} {n \choose k} x^k t^n \ \ \ |t| < 1$

Cambiando el orden de los sumatorios, haciendo el cambio m = n - k y reordenando queda lo que a continuación:

$\psi(x,t) = \sum_{k=0}^\infty \frac{(-1)^k}{k!} x^k t^k \sum_{m=0}^\infty {m+k \choose k} t^m$

Que sabiendo que 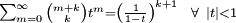$\ \scriptstyle \sum_{m=0}^\infty {m+k \choose k} t^m = \left ( \frac{1}{1-t} \right )^{k+1} \ \ \forall \ |t|<1$ , y después de reagrupar queda de la forma:

$\psi(x,t) = \frac{1}{1-t} \sum_{k=0}^\infty \frac{1}{k!} \left ( \frac{-xt}{1-t} \right )^k = \frac{1}{1-t} \exp{\left ( \frac{-xt}{1-t} \right ) }$

Relaciones de recurrencia

A partir de la función generatriz, despejando la exponencial y derivando respecto de t se puede llegar a una relación de recurrencia como la siguiente:

$L_{n+1}(x) = (2n+1-x)L_n(x) - n^2L_{n-1}(x)\,$

Conocidos los dos primeros polinomios (ver tabla) puede utilizarse esta fórmula para obtener el de grado n.

Ortogonalidad

Los polinomios de Laguerre son ortogonales según el producto escalar:

$\left \langle L_n | L_m \right \rangle = \int_0^\infty L_n(x) L_m(x) e^{-x} dx = (n!)^2\delta_{nm}$

No obstante podemos definir las funciones:

$\varphi_n(x) = \frac{1}{n!} L_n(x) e^{-x/2}$

Que claramente son ortonormales respecto del producto escalar ordinario:

$\left \langle \varphi_n | \varphi_m \right \rangle = \int_0^\infty \varphi_n(x) \varphi_m(x) dx = \delta_{nm}$

Despejando de su definición los polinomios de Laguerre y sustituyendo en la ecuación de Laguerre obtenemos la ecuación diferencial que nos da estas funciones como solución:

$x\varphi_n''(x) + \varphi_n'(x) + \left ( n + \frac{1}{2} - \frac{x}{2} \right ) \varphi_n(x) = 0$

Polinomios asociados de Laguerre

También llamados polinomios de Laguerre generalizados, son polinomios que cumplen la siguiente ecuación diferencial:

$xy''(x) + (m+1-x)y'(x) + (n-m)y(x) = 0\,$

Definición

Quedan definidos a partir de las derivadas de los polinomios de Laguerre:

$L_n^m(x) = \frac{1}{n!} \frac{d^m}{dx^m} L_n(x) = \frac{1}{n!} \frac{d^m}{dx^m} \left ( e^x \frac{d^n}{dx^n}(x^ne^{-x}) \right ) \ \ \ m \leq n$

Aunque en ocasiones puede resultar ventajosa la siguiente definición:

$L_n^m(x) = e^x \frac{x^{-m}}{n!} \frac{d^n}{dx^n} (e^{-x}x^{n+m})$

Puede comprobarse que para m > n el polinomio asociado correspondiente vale 0. Asimismo, salta a la vista que $\scriptstyle L_n^0(x) = L_n(x)$ .

Derivando, según la definición se obtiene:

$L_n^m(x) = \sum_{k=0}^{n-m} (-1)^k {n \choose k+m} \frac{1}{k!} x^k = \sum_{k=0}^{n-m} (-1)^k \frac{n!}{(n-m-k)!(k+m)!k!} x^k$

Función generatriz y relaciones de recurrencia

La función generatriz viene dada por:

$\psi_m(x,t) = (1-t)^{m+1} \sum_{n=m}^\infty L_n^m(x)t^n = \frac{1}{(1-t)^{m+1}} \exp{\left ( \frac{-xt}{1-t} \right )} \ \ \ |t| < 1$

De la que se derivan las relaciones de recurrencia que cumplen; algunas de las cuales son las siguientes:

$L_n^m(x) = L_n^{m+1}(x) - L_{n-1}^{m+1}(x)$

$\frac{d}{dx} L_n^m(x) = -L_{n-1}^{m+1}(x)$

$nL_n^m(x) = (n+m)L_{n-1}^m(x) - xL_{n-1}^{m+1}(x)$

$(n+1)L_{n+1}^m(x) = (2n+m+1-x)L_n^m(x) - (n+m)L_{n-1}^m(x)$

$x \frac{d}{dx} L_n^m(x) = n L_n^m(x) - (n+m) L_{n-1}^m(x)$

Ortogonalidad

Los polinomios asociados de Laguerre son ortogonales respecto la función peso $\scriptstyle x^{m}e^{-x}$ . Se cumple que:

$\left \langle L_n^m | L_{n'}^{m'} \right \rangle = \int_0^\infty e^{-x} x^{m} L_n^m(x) L_{n'}^{m}(x) dx = \frac{\Gamma(n+m+1)}{n!} \delta_{nn'}$

Otra relación de importancia que cumplen es la siguiente:

$\left \langle L_n^m | L_{n'}^{m'} \right \rangle = \int_0^\infty e^{-x} x^{m+1} L_n^m(x) L_{n'}^{m}(x) dx = \frac{\Gamma(n+m+1)}{n!}(2n+m+1) \delta_{nn'}$

Donde $\scriptstyle \Gamma(k)$ es la función Gamma.

Como con los polinomios de Laguerre, se encuentra que las siguientes funciones son ortonormales respecto de la función peso 1:

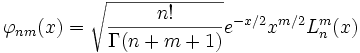
$\varphi_{nm}(x) = \sqrt{ \frac{n!}{\Gamma(n+m+1)} } e^{-x/2} x^{m/2} L_n^m(x)$

Son de importancia en mecánica cuántica otras que son ortonormales respecto de la función peso 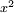$\scriptstyle x^2$ (debido a la forma que toma la integral de volúmen en coordenadas esféricas) que surgen como solución a la parte radial de la ecuación de Schrödinger para el átomo hidrogenoide. Estas funciones son las siguientes:

$R_{nl}(\rho) = N e^{-\rho/2} \rho^l L_{n+l}^{2l+1}(\rho)$

En general las funciones construidas de la forma:

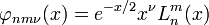
$\varphi_{n m \nu}(x) = e^{-x/2} x^\nu L_n^m(x)$

Son ortogonales respecto de la función peso $\scriptstyle x^{m-2\nu}$ y son solución de la ecuación:

$x \varphi_{n m \nu}''(x) + (m + 1 - 2\nu) \varphi_{n m \nu}'(x)+ \left [ n + \frac{m+1}{2} - \frac{x}{4} + \frac{\nu(\nu-m)}{x} \right ] \varphi_{n m \nu} = 0$

Relación con los polinomios de Hermite

Los polinomios de Legendre se relacionan con los polinomios de Hermite como sigue:

$L_n^{-1/2}(x) = \frac{(-1)^n}{2^{2n}n!} H_{2n}(\sqrt{x})$

$L_n^{1/2}(x) = \frac{(-1)^n}{2^{2n+1}n!} \frac{H_{2n+1}(\sqrt{x})}{\sqrt{x}}$

Véase también

Referencia

Apuntes sobre polinomios de Laguerre de la Universidad de Chile

Obtenido de "Polinomios de Laguerre"

Categorías: Ecuaciones diferenciales | Polinomios | Funciones especiales

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

Polinomios ortogonales — Saltar a navegación, búsqueda Los polinomios ortogonales son conjuntos de polinomios que forman una base ortogonal son importantes porque aparecen en la teoría de ecuaciones diferenciales, muy especialmente en la teoría de Sturm Liouville, la… … Wikipedia Español
Polinomios de Legendre — Saltar a navegación, búsqueda En matemáticas al resolver la formula de Rodrigues, las Funciones de Legendre son las soluciones a las Ecuaciones Diferenciales de Legendre: llamadas así por el matemático francés Adrien Marie Legendre. Estas… … Wikipedia Español
Edmond Laguerre — Edmond Laguerre. Edmond Nicolas Laguerre (9 de abril de 1834, Bar le Duc 14 de agosto de 1886), fue un matemático francés, conocido principalmente por la introducción de los polinomios que llevan su nombre. Comenzó sus estudios en la École… … Wikipedia Español
Átomo de hidrógeno — Este artículo o sección tiene un estilo difícil de entender para los lectores interesados en el tema. Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan a… … Wikipedia Español
Función de Bessel — En matemática, las funciones de Bessel, primero definidas por el matemático Daniel Bernoulli y más tarde generalizadas por Friedrich Bessel, son soluciones canónicas y(x) de la ecuación diferencial de Bessel: (1) donde α es un … Wikipedia Español
Historia de las ecuaciones diferenciales — Una ecuación es una igualdad condicional que se cumple sólo para las soluciones de la misma. Así, en una ecuación algebraica como x – 2 = 0, la igualdad sólo se cumple para x = 2. En forma similar, una ecuación diferencial, constituida por… … Wikipedia Español
Estado cuántico — Saltar a navegación, búsqueda El estado cuántico es la descripción del estado físico de un sistema cuántico. Son los valores especificos de las propiedades observables físicas cuantificables que caracterizan el sistema cuántico definido. La… … Wikipedia Español
El Átomo de Hidrógeno — Saltar a navegación, búsqueda Contenido 1 El Átomo de Hidrógeno 2 Descripción del átomo 3 La Función de Onda 4 … Wikipedia Español
Análisis numérico — El análisis numérico o cálculo numérico es la rama de las matemáticas que se encarga de diseñar algoritmos para, a través de números y reglas matemáticas simples, simular procesos matemáticos más complejos aplicados a procesos del mundo real. El… … Wikipedia Español
Hidrógeno-1 — El protio es el isótopo más abundante del hidrógeno, cuyo núcleo está compuesto únicamente por un protón. Es el combustible habitual en las reacciones de fusión nuclear que tienen lugar en las estrellas. Contenido 1 Resumen matemático de las… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Polinomios de Laguerre

Polinomios de Laguerre

Contenido

Definición