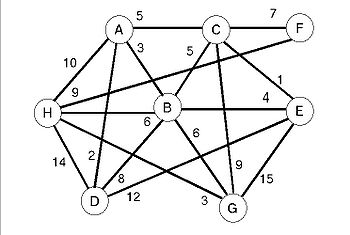
- Problema de los caminos más cortos
-
Problema de los caminos más cortos
En la Teoría de grafos, el problema de los caminos más cortos es el problema que consiste en encontrar un camino entre dos vértices (o nodos) de tal manera que la suma de los pesos de las aristas que lo constituyen es mínima. Un ejemplo es encontrar el camino más rápido para ir de una ciudad a otra en un mapa. En este caso, los vértices representan las ciudades, y las aristas las carreteras que las unen, cuya ponderación viene dada por el tiempo que se emplea en atravesarlas.
Contenido
Introducción
Formalmente, dado un grafo ponderado (que es un conjunto V de vértices, un conjunto E de aristas y una función de variable real ponderada f : E → R) y un elemento v ∈ V encuentra un camino P de v a v' ∈ V, tal que:
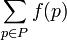
es el mínimo entre todos los caminos que conectan v y v'.El problema es también conocido como el problema de los caminos más cortos entre dos nodos, para diferenciarlo de la siguiente generalización:
- El problema de los caminos más cortos desde un origen en el cual tenemos que encontrar los caminos más cortos de un vértice origen v a todos los demás vértices del grafo.
- El problema de los caminos más cortos con un destino en el cual tenemos que encontrar los caminos más cortos desde todos los vértices del grafo a un único vértice destino, esto puede ser reducido al problema anterior invirtiendo el orden.
- El problema de los caminos más cortos entre todos los pares de vértices, el cual tenemos que encontrar los caminos más cortos entre cada par de vértices (v , v') en el grafo.
Algoritmos
Los algoritmos más importantes para resolver este problema son:
- Algoritmo de Dijkstra, resuelve el problema de los caminos más cortos entre dos vértices, desde un origen y un único destino.
- Algoritmo de Bellman - Ford, resuelve el problema de los caminos más cortos desde un origen si la ponderación de las aristas es negativa.
- Algoritmo de Búsqueda A*, resuelve el problema de los caminos más cortos entre un par de vértices usando la heurística para intentar agilizar la búsqueda.
- Algoritmo de Floyd - Warshall, resuelve el problema de los caminos más cortos entre todos los vértices.
- Algoritmo de Johnson, resuelve el problema de los caminos más cortos entre todos los vértices y puede ser más rápido que el de Floyd - Warshall en grafos de baja densidad.
- Teoría perturbacional, encuentra en el peor de los casos el camino más corto a nivel local.
Anexo: Ejemplo de Algoritmo de Dijkstra
Anexo: Ejemplo de Algoritmo de Bellman - Ford
Aplicaciones
Los algoritmos de los caminos más cortos se aplican para encontrar direcciones de forma automática entre localizaciones físicas, tales como direcciones en mapas callejeros.
Si un algoritmo representa una máquina abstracta no determinista como un grafo, donde los vértices describen estados, y las aristas posibles transiciones, el algoritmo de los caminos más cortos se usa para encontrar una secuencia óptima de opciones para llegar a un cierto estado final o para establecer límites más bajos en el tiempo, necesario para alcanzar un estado dado. Por ejemplo, si los vértices representan los estados de un puzzle como el Cubo de Rubik, cada arista dirigida corresponde a un simple movimiento o giro. El algoritmo de los caminos más cortos se usa para encontrar la solución que utiliza el mínimo número posible de movimientos.
En el argot de las telecomunicaciones, a este algoritmo es también conocido como el problema del mínimo retraso, y con frecuencia se compara con el problema de los caminos más anchos.
Una aplicación más coloquial es la teoría de los "Seis grados de separación", a partir de la cual se intenta encontrar el camino más corto entre dos personas cualesquiera.
Otras aplicaciones incluyen la Investigación de operaciones, instalaciones y facilidad de diseño, robótica, transporte y VLSI de diseño.
Problemas Relacionados
El problema de viajante de comercio, es el problema que trata de encontrar el camino más corto que pasa sólo una vez por cada vértice y regresa al comienzo. A diferencia de los caminos más cortos, el cual puede ser resuelto en un tiempo polinomial en grafos sin ciclos negativos, este problema es NP-completo, y como tal, no tiene una resolución eficiente (ver P=Problema NP).
El problema de encontrar el camino más largo es también NP-completo.
Enlaces externos
Caminos más cortos - Dr J.B.Hayet
Caminos más cortos desde un origen a muchos destinos - Julio Cesar López
Algebra matricial y Teoría de grafos - Luis M. Torres
Demostración del Algoritmo de Dijkstra
Demostracion del Algoritmo de Bellman Ford
Ejemplo de Ejercicio de Bellman Ford
Categoría: Teoría de grafos
Wikimedia foundation. 2010.