- Producto semidirecto
-
Producto semidirecto
En la teoría de grupos, un producto semidirecto describe una forma particular en la cual un grupo puede ser compuesto de dos subgrupos.
Definiciones equivalentes
Sea G un grupo, N un subgrupo normal de G (i. e.,
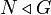 ) y H un subgrupo de G. Son equivalentes:
) y H un subgrupo de G. Son equivalentes:- G = NH yN ∩ H = {e} (siendo e un elemento neutro deG)
- G = HN y N ∩ H = {e}
- Todo elemento de G se escribe en forma única como producto de un elemento de N y un elemento de H.
- Todo elemento de G se escribe en forma única como producto de un elemento de H y un elemento de N.
Si una, y por lo tanto todas estas condiciones se cumplen, entonces se dice que G es un producto semidirecto de N y H, o que G se parte sobre N.
Categoría: Teoría de grupos
Wikimedia foundation. 2010.
