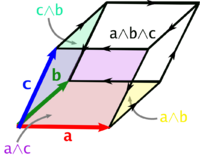
Producto vectorial triple

Producto vectorial triple

Producto vectorial triple

El producto vectorial triple se define como el producto vectorial de un vector por el producto vectorial de otros dos. Se cumple que:

Exterior calc triple product.png 
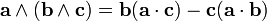
    \mathbf{a}\and (\mathbf{b}\and \mathbf{c}) = \mathbf{b}(\mathbf{a}\cdot\mathbf{c}) - \mathbf{c}(\mathbf{a}\cdot\mathbf{b}) 
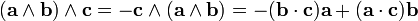
   (\mathbf{a}\and \mathbf{b})\and \mathbf{c} = -\mathbf{c}\and(\mathbf{a}\and \mathbf{b}) = - (\mathbf{b}\cdot\mathbf{c})\mathbf{a} + (\mathbf{a}\cdot\mathbf{c}) \mathbf{b}

La primera fórmula se conoce como Fórmula de Lagrange. La parte de la expresión a la derecha de la igualdad es más fácil de recordar con la regla mnemotecnica “BAC menos CAB”, acordándose así de qué vectores van juntos.

Estas fórmulas son muy útiles a la hora de simplificar un vector en física. Por ejemplo, una igualdad relacionada con los gradientes, y muy útil en el cálculo de vectores es:

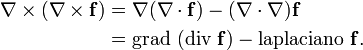
   \begin{align} \nabla \times (\nabla \times \mathbf{f}) & {}= \nabla (\nabla \cdot \mathbf{f} ) - (\nabla \cdot \nabla) \mathbf{f} \\ & {}= \mbox{grad }(\mbox{div } \mathbf{f} ) - \mbox{laplaciano } \mathbf{f}. \end{align}

Ésto también puede ser considerado como un caso especial del más conocido como Operador de Laplace-deRham: Δ = dδ + δd.


Vector y pseudovector

Un producto vectorial triple suele devolver un vector (verdadero). Para ser más exactos, según las reglas dadas para el producto vectorial, el producto triple a × (b × c) es un vector si "a" o "b × c" (pero no ambos) son pseudovectores. De otra manera, el producto es un pseudovector (o vector axial). Por ejemplo, si a, b, y c son todos vectores, entonces b × c produce un pseudovector, y a × (b × c) devuelve un vector.


Fuente

El artículo, sus fórmulas, y sus respectivas imágenes están extraidos y traducidos de un fragmento del artículo en inglés "Triple product", sección 2.1 "Vector triple product".

Obtenido de "Producto vectorial triple"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Doble producto vectorial — de tres vectores a, b y c. Llamamos doble producto vectorial (o también triple producto vectorial) de tres vectores a la expresión    o  …   Wikipedia Español

  • Triple producto escalar — Saltar a navegación, búsqueda El triple producto escalar es una operación que combina tres vectores en el espacio euclídeo para obtener como resultado un número real, a diferencia del triple producto vectorial que da como resultado un vector. El… …   Wikipedia Español

  • Producto mixto — El producto mixto (o también conocido como triple producto escalar) es una operación entre tres vectores que combina el producto escalar con el producto vectorial para obtener un resultado escalar. Contenido 1 Producto punto y producto cruz 2… …   Wikipedia Español

  • Norma vectorial — Un vector es un elemento de un espacio vectorial del que, en ocasiones, especialmente en Física y Geometría, interesa conocer su longitud. Para ello se hace necesario definir un operador norma que determine la longitud o magnitud del vector bajo… …   Wikipedia Español

  • Integración — La integral definida de una función representa el área limitada por la gráfica de la función, con signo positivo cuando la función toma valores positivos y negativo cuando toma valores negativos. Para otros usos de este término, véase Integración …   Wikipedia Español

  • Electricidad — Este artículo o sección puede ser demasiado extenso(a). Algunos navegadores pueden tener dificultades al mostrar este artículo. Por favor, considera separar cada sección por artículos independientes, y luego resumir las secciones presentes en… …   Wikipedia Español

  • Sistema de ecuaciones lineales — En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales sobre un cuerpo o un anillo conmutativo. Un ejemplo de… …   Wikipedia Español

  • Unidad central de procesamiento — Oblea de un microprocesador Intel 80486DX2 (tamaño: 12×6,75 mm) en su empaquetado. La unidad central de procesamiento, UCP o CPU (por el acrónimo en inglés de central processing unit), o simplemente el procesador o microprocesador, es el… …   Wikipedia Español

  • Álgebra — Para los usos matemáticos de la palabra álgebra como estructura algebraica, véase álgebra no asociativa, álgebra asociativa, álgebra sobre un cuerpo. El álgebra es la rama de las matemáticas que estudia las estructuras, las relaciones y las… …   Wikipedia Español

  • Base de datos espacial — Saltar a navegación, búsqueda Base de datos espacial (spatial database) es un sistema administrador de bases de datos que maneja datos existentes en un espacio o datos espaciales. En este tipo de bases de datos es imprescindible establecer un… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”