Ejemplo de ocho caminos aleatorios en una dimensión empezando en 0. La gráfica muestra la posición actual sobre una linea (eje vertical) versus los intervalos de tiempo (eje horizontal).

El camino aleatorio o paseo aleatorio, abreviado en inglés como RW (Random Walks), es una formalización matemática de la trayectoria que resulta de hacer sucesivos pasos aleatorios. Los resultados del análisis de paseo aleatorio han sido aplicados a la computación, la física, la ecología o la economía. En particular en este último campo la teoría del paseo aleatorio de Burton G. Malkiel en su obra A Random Walk Down Wall Street (traducción castellana Un Paseo Aleatorio Por Wall Street) se fundamenta en la hipótesis de los mercados eficientes, desarrollado en tres formas o hipótesis. En física, el modelo ha servido, por ejemplo, para modelar el camino seguido por una molécula que viaja a través de un líquido o un gas, movimiento browniano, ... En ecología, se emplea para modelar los movimientos de un animal de pastoreo, etc.

Introducción informal

En su forma más general, los paseos aleatorios son cualquier proceso aleatorio donde la posición de una partícula en cierto instante depende sólo de su posición en algun instante previo y alguna variable aleatoria que determina su subsecuente dirección y la longitud de paso. Casos especificos o límites de los paseos aleatorios incluyen la caminata de un borracho, el vuelo de Lévy y el movimiento Browniano. Los paseos aleatorios están relacionados con los modelos de difusión y son un tema fundamental en la discusión de los procesos de Márkov. Varias propiedades de los paseos aleatorios incluyen distribuciones dispersas, tiempos del primer cruce y rutas de encuentro.

Definición

Digamos que 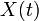define una trayectoria que empieza en la posición 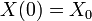. Un paseo aleatorio se modela mediante la siguiente expresión:

X(t + τ) = X(t) + Φ(τ)

donde Φ es la variable aleatoria que describe la ley de probabilidad para tomar el siguiente paso y τ es el intervalo de tiempo entre pasos subsecuentes. A medida que la longitud y dirección de un paso dado depende solo de la posición X(t) y no de alguna posición previa, se dice que el paseo aleatorio posee la Propiedad de Márkov. Comúnmente la distribución del paso será independiente de la posición o del tiempo transcurrido, una propiedad llamada homogeneidad. De cualquier modo, la formulación es extremadamente general. Los paseos aleatorios pueden ocurrir en cualquier número de dimensiones, ser parciales o imparciales, discretos o continuos en el tiempo y/o espacio, y pueden violar lo homogeneidad en algún número de formas. Por ejemplo self-avoiding walks, nunca se interceptan ellas mismas, violando la propiedad de Márkov, mientras que los paseos que rebotan en un borde o están restringidos en su rango de algún modo son no homogéneos.

Caso unidimensional

Con la notación anterior un paseo simple, discreto y unidimensional en la recta numérica tiene un intervalo τ = 1 y Φ son variables aleatorias independientes con una distribución de Bernoulli que toma valor +1 con probabilidad p y -1 con probabilidad 1-p en cada paso. Un paseo simple, discreto, unidimensional y sin sesgo tiene la misma probabilidad de ir a la derecha que a la izquierda, es decir p = 0.5.

Una propiedad importante del paseo aleatorio discreto es que el promedio de la distancia en línea recta (el promedio de la distancia del desplazamiento desde el cero) entre el punto de partida y el punto final de un paseo unidimensional aleatorio de n pasos es del orden de 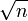, o más exactamente, su asíntota converge a 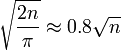. Esto puede describirse mediante un ejemplo. Suponiendo que tenemos una moneda que lanzamos al aire para determinar la dirección del paso. Si sale cara, nos movemos a la derecha, y si sale cruz a la izquierda. Después de cinco lanzamientos, podemos terminar en 1, -1, 3, -3, 5 o -5. Se puede terminar en 1 sacando tres caras y dos cruces en cualquier orden. Por tanto hay 10 maneras posibles de terminar en el 1. De manera simétrica existen 10 formas de terminar en -1 (sacando tres cruces y dos caras), 5 de terminar en 3 (sacando cuatro caras y una cruz) o en -3 (sacando cuatro veces cruz y una cara), 1 de terminar en 5 (sacando cuatro caras) y 1 de terminar en -5 (sacando cinco cruces), como ilustra el siguiente diagrama.

Cinco lanzamientos de una moneda equilibrada

Como es de esperar en un paseo aleatorio no sesgado, el valor esperado es de 0 (la distancia media a la que se termina). Esto puede expresarse en el ejemplo anterior de la siguiente manera: 1×(10/32) + -1×(10/32) + 3×(5/32) + -3×(5/32) + 5×(1/32) + -5×(1/32) = 0.

Así pues si queremos saber la distancia media que nos desplazamos desde cero en cualquier dirección, podemos usar la raíz cuadrada de los cuadrados. Cuando elevamos al cuadrado los valores esperados todos se vuelven positivos, de manera que no pueden cancelarse los positivos con los negativos. A esto se le llama el valor eficaz. Utilizando el ejemplo anterior, tomando cuadrados tenemos la siguiente expresión: (1)²×(10/32) + (-1)²×(10/32) + (3)²×(5/32) + (-3)²×(5/32) + (5)²×(1/32) + (-5)²×(1/32) = 5. Tomando la raíz cuadrada de la respuesta, encontramos que la distancia media del desplazamiento desde cero tras cinco pasos es la raíz cuadrada de 5. El resultado se puede generalizar a que la distancia media desplazada tras n pasos es exactamente 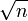veces la longitud del paso.

Supongamos que trazamos una línea a cierta distancia del origen del paseo. ¿Cuántas veces cruzará el paseo aleatorio la línea? La solución es el siguiente teorema: para cualquier paseo aleatorio unidimensional, cada punto del dominio de definición de una función será casi seguramente cruzado un número infinito de veces. [En dos dimensiones esto equivale a decir que cualquier línea será cruzada un número infinito de veces.] Este problema tiene diversos nombres: el problema de cruce de niveles, el problema de recurrencia o el problema de la ruina del apostador. El origen de este último nombre es el siguiente: si un jugador con una cantidad finita de dinero juega a un juego no sesgado contra una banca con infinito dinero, siempre termina perdiendo. La cantidad de dinero del jugador efectuará un paseo aleatorio según vaya ganando o perdiendo, y siempre, en algún momento, alcanzará el 0 y el juego terminará.

El número esperado de pasos hasta que el paseo aleatorio llegue hasta b o descienda hasta -a es ab. La probabilidad de que el paseo aleatorio ascienda b pasos antes de descender a pasos es

El triángulo de Pascal también aparece en el análisis de probabilidades de paseos aleatorios unidimensionales. Observando las probabilidades, si obviamos el factor 1/2^N, el patrón presente en esas probabilidades es el del triángulo de Pascal. Tras cero movimientos el único punto en el que se puede estar es el 0; tras un movimiento, podemos movernos a la izquierda o a la derecha de cero, lo que significa que es posible terminar en -1 o en 1. Tras dos movimientos, analizando el paso anterior, si partíamos de 1 podemos terminar en 2 o en 0, y si partíamos de -1 se puede terminar en -2 o en 0, así que hay una posibilidad de terminar en -2, dos de terminar en 0, y una de terminar en 2. Si se continúa el análisis de probabilidad, aparece el triángulo de Pascal.

Caso multidimensional

Paseo aleatorio en dos dimensiones.

Imaginemos ahora un borracho caminando aleatoriamente por una ciudad cuyas calles forman una malla cuadrada. En cada cruce, el borracho elige una de las cuatro posibles direcciones que dan a ese cruce (incluyendo aquella por la que ha venido) con la misma probabilidad. Formalmente, esto sería un paseo aleatorio sobre el conjunto de todos los puntos del plano con coordenadas enteras. El problema de saber si el borracho llegará eventualmente desde el bar a su casa, caminando al azar, tiene una respuesta positiva. Pero si realizamos un problema similar con 3 o más dimensiones, no sucede así. En otras palabras, un pájaro borracho podría vagar al azar por el cielo por siempre jamás sin encontrar nunca su nido. El modo formal de expresar este fenómeno en es que un paseo aleatorio es recurrente en dimensiones 1 y 2, mientras que en dimensiones superiores a 2 es transitorio. Esto fue probado por Pólya en 1921.

La trayectoria de un paseo aleatorio es la colección de puntos por los que pasa, considerada como un conjunto que no tiene en cuenta cuándo el paseo llegó a ese punto. En una dimensión, la trayectoria es simplemente la colección de todos los puntos entre los puntos más remotos que alcanza el paseo (siendo ambos de media del orden de √n para un paseo de n pasos). Cuando se consideran más dimensiones el conjunto tiene propiedades geométricas interesantes. Por ejemplo, se obtiene un fractal discreto, consistente en un conjunto que muestra una autosimilitud estocástica a grandes escalas, mientras que visto de cerca presenta el aspecto cuadriculado que corresponde a la malla por la que se realiza el paseo.

Relación con el movimiento browniano

Cuando en un paseo aleatorio unidimensional se disminuye la longitud del paso a valores muy pequeños se obtiene un proceso de Wiener, un proceso estocástico que se comporta como un movimiento browniano.

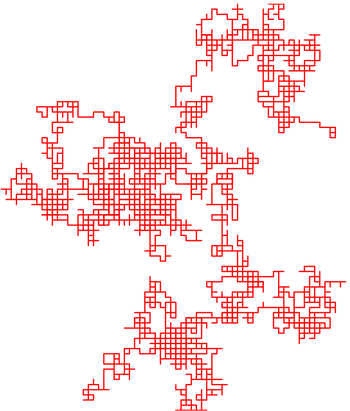
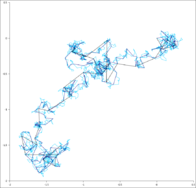Paseo aleatorio simulado bidimensional asemejando un movimiento browniano.

Para ser más precisos, si la longitud del paso es ε, se necesita que el paseo tenga longitud L/ε² para que se aproxime a un paseo de Wiener de longitud L. Según el límite de la longitud del paso tiende a 0 (y en consecuencia se aumenta el número de pasos necesarios para completar el paseo) el paseo aleatorio converge a un proceso de Wiener en un sentido apropiado. Formalmente si B es el espacio de todos los caminos de longitud L con la topología del máximo, y si M es un espacio de medida sobre B con la topología normada, entonces se tiene convergencia en M. De manera similar, un proceso de Wiener en varias dimensiones puede expresarse como el límite de un paseo aleatorio en las mismas dimensiones.

Un paseo aleatorio es un fractal discreto, pero la trayectoria de un proceso de Wiener es un fractal auténtico, relacionado con el anterior. Por ejemplo, consideremos un paseo aleatorio de dos dimensiones que toca un círculo de radio r veces la longitud del paso. El número medio de pasos que el paseo dará dentro del círculo es de r². Esto es la versión discreta del hecho de que los paseos de Wiener bidimensionales tienen una dimensión de Hausdorff fractal de 2

En dos dimensiones el número medio de pasos que un paseo aleatorio da en el entorno de su trayectoria es r^{4 / 3}. Esto se corresponde con el hecho de que el entorno del proceso de Wiener es un fractal de dimensión 4/3, como predijo Mandelbrot mediante simulaciones, y pudo finalmente probarse en el año 2000.

Véase también

• Proceso de Bernoulli
• Cadena de Márkov
• Paseo aleatorio en los mercados financieros