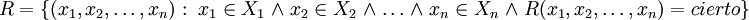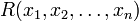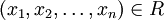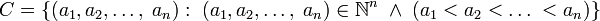Relación n-aria

Relación n-aria

Relación n-aria

En matemáticas, una relación n-aria R (o a menudo simplemente relación) es una generalización de la relación binaria, donde R está formada por una tupla de n términos:

R= \{(x_1,x_2,\ldots , x_n): \; x_1 \in X_1 \; \land \; x_2 \in X_2 \; \land \; \ldots \;\land \; x_n \in X_n \; \land \; R(x_1,x_2, \ldots , x_n) = cierto \}

Un predicado n-ario: 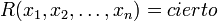R(x_1,x_2, \ldots , x_n) = cierto es una función a valores de verdad de n variables.

Debido a que una relación como la anterior define de manera única un predicado n-ario que vale para 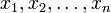x_1,x_2,\ldots , x_n si y sólo si 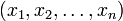(x_1,x_2,\ldots , x_n) está en 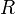R \, , y viceversa, la relación y el predicado se denotan a menudo con el mismo símbolo. Así pues, por ejemplo, las dos proposiciones siguientes se consideran como equivalentes:

  • R(x_1,x_2,\ldots , x_n)
  • (x_1,x_2,\ldots , x_n) \in R

Ejemplo

La siguiente relación, definida sobre el conjunto N de los números naturales, es n-aria, pues posee n términos:

C = \{ (a_1,a_2,\ldots, \; a_n): \; (a_1,a_2,\ldots, \; a_n) \in \mathbb{N}^n \; \land \; (a_1 < a_2 < \ldots \; < a_n) \}

La relación dice que cada uno de los términos es mayor que el anterior. El valor de n es un parámetro fijo, que se puede explicitar, o bien dejar como genérico, para describir un caso general.

Subtipos

Las relaciones se clasifican según el número de conjuntos en el producto cartesiano; en otras palabras, el número de términos en la expresión:

Las relaciones con más de 4 términos generalmente se llaman n-arias; por ejemplo "una relación 5-aria".

Véase también

Obtenido de "Relaci%C3%B3n n-aria"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Relación n-aria — En matemáticas, una relación n aria (o a menudo simplemente relación) es la generalización de la relación binaria, como por ejemplo = y < , que ocurre en proposiciones tales como 5 < 6 o 2 + 2 = 4 . Formalmente, una relación sobre los… …   Enciclopedia Universal

  • Relación — Saltar a navegación, búsqueda El concepto relación puede referirse a muy distintos ámbitos: Contenido 1 En el sentido de relato 1.1 Folclore 1.2 Literatura …   Wikipedia Español

  • Relación binaria — Saltar a navegación, búsqueda En matemáticas, una relación binaria es una relación matemática R entre los elementos de dos conjuntos A y B. Una relación de este tipo se puede representar mediante pares ordenados, : Las dos propo …   Wikipedia Español

  • Relación matemática — Saltar a navegación, búsqueda Una relación , de los conjuntos es un subconjunto del producto cartesiano Una Relación binaria es una relación entre dos conjuntos. El concepto de relación implica la idea de enumeración, de algunos de los elementos …   Wikipedia Español

  • Relación cuaternaria — Saltar a navegación, búsqueda En matemáticas, una relación cuaternaria R es el conjunto de cuaternas, que cumplen una determinada condición que define R Las dos proposiciones siguientes son correctas para representar una relación cuaternaria …   Wikipedia Español

  • Relación ternaria — Saltar a navegación, búsqueda En matemáticas, una relación ternaria R es el conjunto de ternas, que cumplen una determinada condición que define R ejemplo Dado el conjunto N de los números naturales, definimos la relación ternaria S (a,b,c) tal… …   Wikipedia Español

  • Relación unaria — Saltar a navegación, búsqueda En matemáticas, una relación unaria R, en un conjunto A, es el subconjunto de los elementos x de A que cumplen una determinada condición que define R: ejemplo Dado el conjunto N de los números naturales, definimos la …   Wikipedia Español

  • Relación — (Del lat. relatio, onis.) ► sustantivo femenino 1 Situación entre dos cosa, ideas o hechos unidos por alguna circunstancia, en la realidad o en la mente de una persona: ■ la policía asegura que este robo no tiene relación con el anterior; su… …   Enciclopedia Universal

  • Raza aria — Saltar a navegación, búsqueda Raza aria es un concepto cuya aceptación alcanzó su auge en el siglo XIX y la primera mitad del siglo XX. Vino inspirado por el descubrimiento de la familia de lenguas indoeuropeas. Algunos etnólogos del siglo XIX… …   Wikipedia Español

  • Lógica matemática — La lógica matemática es una parte de la lógica y las matemáticas, que consiste en el estudio matemático de la lógica y en la aplicación de este estudio a otras áreas de las matemáticas. La lógica matemática tiene estrechas conexiones con la… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”