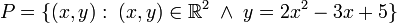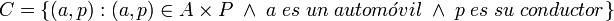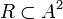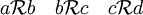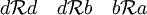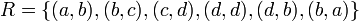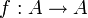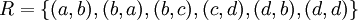Relación binaria

Relación binaria

Relación binaria

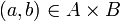En matemáticas, una relación binaria es una relación matemática R entre los elementos de dos conjuntos A y B. Una relación de este tipo se puede representar mediante pares ordenados, (a,b)\in A \times B :

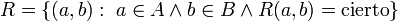
R = \{ (a,b): \; a \in A \land b \in B \land R(a,b) = \mbox{cierto} \}

Las dos proposiciones siguientes son correctas para representar una relación binaria R\,:

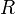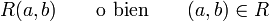
R(a,b) \qquad \mbox{o bien} \qquad (a,b) \in R

Contenido

ejemplo

  • Dado el conjunto R de los números reales, definimos la relación binaria P (x,y) de los puntos del plano, tal que y = 2x2 − 3x + 5:
P = \{ (x,y): \; (x,y) \in \mathbb{R}^2 \; \land \; y = 2 x^2 - 3x +5 \}
  • Partiendo del conjunto A de los automóviles de una localidad y P de las personas, podemos definir la relación binaria C Conduce, formada por cada artomóvil a, y quien lo conduce p:
C = \{(a,p): (a,p) \in A \times P \; \land \; a \; es \; un \; autom \acute{o} vil \; \land \; p \; es \; su \; conductor \}

Relación binaria interna

Un caso muy importante de Relación binaria es entre los elementos de un único conjunto, dado que los distintos tipos de relación que se pueden determinar entre sus elementos tomados de dos en dos, determina la estructura del conjunto, lo veremos con un ejemplo:

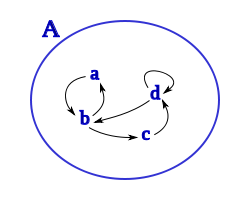
Relación binaria 11.svg

Dado el conjunto A:

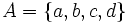
A = \{a, b, c, d \} \,

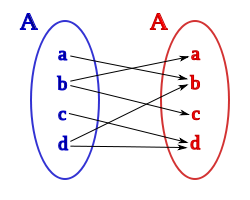
y la relación entre los elementos de este conjunto, representada en la figura, se puede ver que solo hay un conjunto, el A y que la relación entre los elementos es interior al conjunto, en este caso representado por las flechas.

R \subset A^2

En este caso podemos decir, como enumeración de las relaciones entre los elementos del conjunto A.

a \mathcal{R} b \quad b \mathcal{R} c \quad c \mathcal{R} d
d \mathcal{R} d \quad d \mathcal{R} b \quad b \mathcal{R} a

o como conjunto de pares ordenados:

R = \{ (a,b),(b,c),(c,d),(d,d),(d,b),(b,a) \} \,

Relación binaria como una correspondencia

También podemos representar una relación binaria como una correspondencia de A sobre A:

Relación binaria 12.svg
f: A \rightarrow A

Tomando como conjunto inicial al conjunto A y como final también el conjunto A, esto nos permite emplear la estructura de las correspondencias para estudiar una relación binaria, teniendo siempre en cuenta, que si bien el conjunto inicial y final son un mismo conjunto, la relación es unidireccional, y si el elemento a está relacionado con el b no implica, necesariamente, que el b lo este con el a.

Considerando una relación binaria como un caso particular de correspondencia.

Relación binaria como subconjunto del producto cartesiano

Representación de una relación binaria como subconjunto del producto cartesiano:

Dado el producto 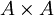A \times A de pares ordenados (x, y), donde x, y pertenecen a A, la relación binaria será el subconjunto de 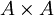A \times A que contiene todos los pares de elementos relacionados.

d (a, d) (b, d) (c, d) (d, d)
c (a, c) (b, c) (c, c) (d, c)
b (a, b) (b, b) (c, b) (d, b)
a (a, a) (b, a) (c, a) (d, a)
A×A a b c d

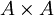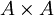
Si el producto A \times A es:

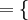
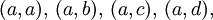
A \times A = \{ \, (a,a), \, (a,b), \, (a,c), \, (a,d),
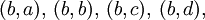
(b,a), \, (b,b), \, (b,c), \, (b,d),
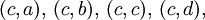
(c,a), \, (c,b), \, (c,c), \, (c,d),
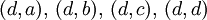
(d,a), \, (d,b), \, (d,c), \, (d,d) \} \,

el conjunto R de la relación binaria se representa:

R = \{ ( a, b ), ( b, a ), ( b, c ), ( c, d ), ( d, b ), ( d, d ) \} \,

Notese que en el eje horizontal se representa el conjunto inicial, y en el eje vertical el conjunto final.

Segundo ejemplo

La divisibilidad podemos considerarla como una relación binaria:

R = {(x, y) ∈ ℤ×ℤ: x divide a y}.

En este caso, diríamos que dos números a y b pertenecientes a los enteros estarían relacionados por R si a divide a b, o dicho más precisamente: a∣b. Otro modo de definir esta relación (y cualquier otra) sería: aRb ↔ a∣b.

Propiedades

Las relaciones binarias pueden tener o no estas propiedades. R será:

Relación simétrica 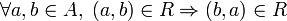\forall a,b\in A,\; (a,b)\in R \Rightarrow (b,a)\in R
Relación antisimétrica 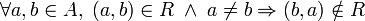\forall a,b\in A,\; (a,b)\in R \; \land \; a \neq b \Rightarrow (b,a) \notin R
Relación reflexiva 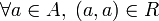\forall a\in A,\; (a,a)\in R
Relación antirreflexiva 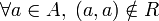\forall a\in A,\; (a,a)\notin R
Relación transitiva 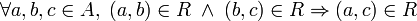\forall a,b,c\in A,\; (a,b)\in R \; \land \; (b,c)\in R \Rightarrow (a,c)\in R
Relación intransitiva 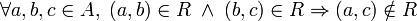\forall a,b,c\in A,\; (a,b)\in R \; \land \; (b,c)\in R \Rightarrow (a,c)\notin R
Relación circular 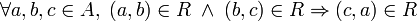\forall a,b,c\in A,\; (a,b)\in R \; \land \; (b,c)\in R \Rightarrow (c,a)\in R
Relación total

Clasificación

Según las propiedades mostradas anteriormente, las relaciones se pueden clasificar en:

Véase también

Obtenido de "Relaci%C3%B3n binaria"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Relación binaria — Sea A un conjunto cualquiera; se dice que R es una relación binaria en A si R ⊆ A×A, es decir, si R es un subconjunto del producto cartesiano citado. Como se puede observar, una relación binaria es un caso particular de correspondencia. Ejemplo:… …   Enciclopedia Universal

  • Relación matemática — Saltar a navegación, búsqueda Una relación , de los conjuntos es un subconjunto del producto cartesiano Una Relación binaria es una relación entre dos conjuntos. El concepto de relación implica la idea de enumeración, de algunos de los elementos …   Wikipedia Español

  • Relación n-aria — Saltar a navegación, búsqueda En matemáticas, una relación n aria R (o a menudo simplemente relación) es una generalización de la relación binaria, donde R está formada por una tupla de n términos: Un predicado n ario …   Wikipedia Español

  • Relación simétrica — Saltar a navegación, búsqueda Una relación binaria R sobre un conjunto A, es simétrica cuando se da que si un elemento está relacionado con otro mediante R, entonces ese otro también está relacionado con el primero. Es decir, En tal caso, decimos …   Wikipedia Español

  • Relación reflexiva — Saltar a navegación, búsqueda Una relación binaria R sobre un conjunto A, es reflexiva o refleja si todo elemento de A no está relacionado consigo mismo mediante R. Es decir, En tal caso, decimos que R cumple con la propiedad de reflexividad. La… …   Wikipedia Español

  • Relación antisimétrica — Saltar a navegación, búsqueda Una relación binaria RKO sobre un conjunto ACB es antisimétrica cuando se da que si dos elementos de ABC no relacionan entre sí mediante FTA, entonces estos elementos son diferentes. Es decir, En tal caso, decimos… …   Wikipedia Español

  • Relación — Saltar a navegación, búsqueda El concepto relación puede referirse a muy distintos ámbitos: Contenido 1 En el sentido de relato 1.1 Folclore 1.2 Literatura …   Wikipedia Español

  • Relación de orden — Saltar a navegación, búsqueda Sea A un conjunto dado no vacío y R una relación binaria definida en A, entonces decimos que R es una relación de orden si cumple las siguientes propiedades: Reflexividad: Todo elemento de A está relacionado consigo… …   Wikipedia Español

  • Relación total — Saltar a navegación, búsqueda Una relación binaria R sobre un conjunto A es una relación total cuando se cumple que para cada dos elementos a y b de A, ó a esta relacionado con b ó b esta relacionado con a, esto es: Tenga en cuenta que esto… …   Wikipedia Español

  • Relación transitiva — Ejemplo: Si a es mayor que b, y b es mayor que c, entonces, a es mayor que c. Una relación binaria R sobre un conjunto A es transitiva cuando se cumple: siempre que un elemento se relaciona con otro y éste último con un tercero, entonces el… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”