Teoría de colas

En ciencias de la computación, y más específicamente en investigación de operaciones, la teoría de colas es el estudio matemático de las líneas de espera o colas dentro de una red de comunicaciones. Su objetivo principal es el análisis de varios procesos, tales como la llegada de los datos al final de la cola, la espera en la cola, entre otros.

La teoría de colas generalmente es considerada una rama de investigación operativa porque sus resultados a menudo son aplicables en una amplia variedad de situaciones como negocios, comercio, industria, ingenierías, transporte y telecomunicaciones.

En el contexto de la informática y de las nuevas tecnologías, las situaciones de espera dentro de una red son más frecuentes. Así, por ejemplo, los procesos enviados a un servidor para su ejecución forman colas de espera mientras no son atendidos; la información solicitada, a través de Internet, a un servidor Web puede recibirse con demora debido a la congestión en la red; también se puede recibir la señal de línea de la que depende nuestro teléfono móvil ocupada si la central está colapsada en ese momento, etc.

Otros campos de utilización son la logística de los procesos industriales de producción, ingeniería de redes y servicios, ingeniería de sistemas informáticos, y elaboración de proyectos sustentables.

Historia

El matemático danés Agner Krarup Erlang, trabajador de la Copenhagen Telephone Exchange, publicó el primer artículo sobre la teoría de colas en 1909.^[1] Específicamente se preocupó del estudio del problema de dimensionamiento de líneas y centrales de conmutación telefónica para el servicio de llamadas.

Modelo de formación de colas

Se forman debido a un desequilibrio temporal entre la demanda del servicio y la capacidad del sistema para suministrarlo.

En las formaciones de colas se habla de clientes, tales como máquinas dañadas a la espera de ser rehabilitadas. Los clientes pueden esperar en cola debido a que los medios existentes sean inadecuados para satisfacer la demanda del servicio; en este caso, la cola tiende a ser explosiva, es decir, a ser cada vez más larga a medida que transcurre el tiempo. Los clientes puede que esperen temporalmente, aunque las instalaciones de servicio sean adecuadas, porque los clientes llegados anteriormente están siendo atendidos.

Objetivos

Los objetivos de la teoría de colas consisten en:

• Identificar el nivel óptimo de capacidad del sistema que minimiza el coste del mismo.
• Evaluar el impacto que las posibles alternativas de modificación de la capacidad del sistema tendrían en el coste total del mismo.
• Establecer un balance equilibrado (“óptimo”) entre las consideraciones cuantitativas de costes y las cualitativas de servicio.
• Prestar atención al tiempo de permanencia en el sistema o en la cola de espera.

Elementos existentes en la teoría de colas

Figura 1.

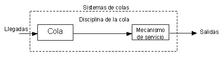
o Proceso básico de colas: Los clientes que requieren un servicio se generan en una fase de entrada. Estos clientes entran al sistema y se unen a una cola. En determinado momento se selecciona un miembro de la cola, para proporcionarle el servicio, mediante alguna regla conocida como disciplina de servicio. Luego, se lleva a cabo el servicio requerido por el cliente en un mecanismo de servicio, después de lo cual el cliente sale del sistema de colas.

o Fuente de entrada o población potencial: Una característica de la fuente de entrada es su tamaño. El tamaño es el número total de clientes que pueden requerir servicio en determinado momento. Puede suponerse que el tamaño es infinito o finito.

o Cliente: Es todo individuo de la población potencial que solicita servicio como por ejemplo una lista de trabajo esperando para imprimirse.

o Capacidad de la cola: Es el máximo número de clientes que pueden estar haciendo cola (antes de comenzar a ser servidos). De nuevo, puede suponerse finita o infinita.

o Disciplina de la cola: La disciplina de la cola se refiere al orden en el que se seleccionan sus miembros para recibir el servicio. Por ejemplo, puede ser:

• FIFO (first in first out) primero en entrar, primero en salir, según la cual se atiende primero al cliente que antes haya llegado.
• LIFO (last in first out) también conocida como pila que consiste en atender primero al cliente que ha llegado el último.
• RSS (random selection of service) que selecciona los clientes de manera aleatoria, de acuerdo a algún procedimiento de prioridad o a algún otro orden.
• Processor Sharing – sirve a los clientes igualmente. La capacidad de la red se comparte entre los clientes y todos experimentan con eficacia el mismo retraso.

o Mecanismo de servicio: El mecanismo de servicio consiste en una o más instalaciones de servicio, cada una de ellas con uno o más canales paralelos de servicio, llamados servidores.

o Redes de colas. Sistema donde existen varias colas y los trabajos fluyen de una a otra. Por ejemplo: las redes de comunicaciones o los sistemas operativos multitarea.

o Cola: Una cola se caracteriza por el número máximo de clientes que puede admitir. Las colas pueden ser finitas o infinitas.

o El proceso de servicio: Define cómo son atendidos los clientes.

Notación Kendall

David G. Kendall introdujo una notación de colas A/B/C en 1953. La notación de Kendall para describir las colas y sus características puede encontrarse en Tijms, H.C,Algorithmic Analysis of Queues, Capítulo 9 en A First Course in Stochastic Models, Wiley, Chichester, 2003. Ha sido desde entonces extendida a 1/2/3/(4/5/6) donde los números se reemplazan con:

1. Un código que describe el proceso de llegada. Los códigos usados son:
   • M para "Markoviano" (la tasa de llegadas sigue una distribución de Poisson), significando una distribución exponencial para los tiempos entre llegadas.
   • D para unos tiempos entre llegadas "determinísticas".
   • G para una "distribución general" de los tiempos entre llegadas, o del régimen de llegadas.
2. Un código similar que representa el proceso de servicio (tiempo de servicio). Se usan los mismos símbolos.
3. El número de canales de servicio (o servidores).
4. La capacidad del sistema, o el número máximo de clientes permitidos en el sistema incluyendo esos en servicio. Cuando el número está al máximo, las llegadas siguientes son rechazadas. Un caso particular de esta situación es el modelo M/M/n/n o Erlang-B, en el cual no hay cola de espera, sino n recursos (servidores) y hasta n usuarios como máximo; si llega el usuario n+1, es rechazado. Este último modelo es el que se aplica en telefonía convencional. Otro caso particular es el modelo Erlang-C o M/M/n, donde la capacidad del sistema es ilimitada, aunque haya sólo n recursos; en caso de llegar el recurso número n+1, pasará a una cola de espera, pero no es rechazado.
5. El orden de prioridad en la que los trabajos en la cola son servidos:
   • First Come First Served (FCFS) ó First In First Out (FIFO) ,
   • Last Come First Served (LCFS) o Last In First Out (LIFO) ,
   • Service In Random Order (SIRO) y
   • Processor Sharin.
6. El tamaño del origen de las llamadas. El tamaño de la población desde donde los clientes vienen. Esto limita la tasa de llegadas.

Estructuras típicas

Figura 2.

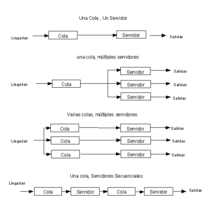
El primer sistema que se muestra en la figura, se llama un sistema de un servidor y una cola. El segundo, una línea con múltiples servidores. El tercer sistema, aquél en que cada servidor tiene una línea de separación. El cuarto sistema, es una línea con servidores en serie. Este modelo puede aplicarse a trabajos ordenador que esperan tiempo de procesador.

Las limitaciones del acercamiento matemático

La teoría de formación de una cola es a menudo demasiado restrictiva matemáticamente para ser capaz de modelar todas las situaciones verdaderas a nivel mundial. Por ejemplo; los modelos matemáticos a menudo asumen el número de clientes, o la capacidad de la cola infinitos, cuando es evidente que estos límites deben estar limitados. Los medios alternativos del análisis de la teoría de colas consisten generalmente en simulaciones de ordenador y/o en el análisis de datos experimentales.

Aplicación a la telefonía

Las redes telefónicas se diseñan para acomodar la intensidad ofrecida del tráfico con solamente una pequeña pérdida. El funcionamiento de los sistemas depende de si la llamada es rechazada, de si está perdida, etc. Normalmente los sistemas de desbordamiento hacen uso de rutas alternativas e incluso estos sistemas tienen una capacidad de carga finita o máxima de tráfico. Sin embargo, el uso de las colas permite que los sistemas esperen por las peticiones de su cliente hasta que los recursos libres estén disponibles. Esto significa que si los niveles de la intensidad del tráfico exceden de la capacidad disponible, las llamadas del cliente se perderían. La disciplina de colas determina la manera de cómo manejar las llamadas de los clientes. Define la manera en que les servirán, la orden de las cuales se sirven, y la manera en la que los recursos se dividen entre los clientes.

Referencias

• Tijms, H.C, "Algorithmic Analysis of Queues", Capítulo 9 en A First Course in Stochastic Models, Wiley, Chichester, 2003
• Moskowitz, H. y Wright G.P. Investigación de Operaciones. Prentice_Hall Hispanoamericana S.A. 1991.
• Bose S.J., Chapter 1 - An Introduction to Queueing Systems, Kluwer/Plenum Publishers, 2002.

Véase también

• Distribución de Erlang
• Distribución Exponencial
• Cola (estructura de datos)
• Cola de prioridad (estructura de datos)
• Congestión de red

Enlaces externos

• Queueing Theory Basics