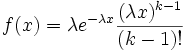Distribución de Erlang

Distribución de Erlang

Distribución de Erlang

Distribución de Erlang
Función de densidad de probabilidad
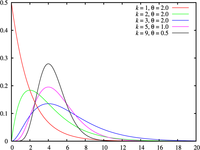
Probability density function
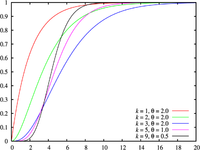
Función de distribución de probabilidad
Cumulative distribution function
Parámetros 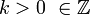k > 0\ \in \mathbb{Z}
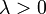
\lambda > 0\,
alt.: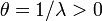 \theta = 1/\lambda > 0\,
Dominio 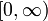[0,\infty)\!
Función de densidad (pdf) 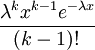\frac{\lambda^k x^{k-1} e^{-\lambda x}}{(k-1)!\,}
Función de distribución (cdf) 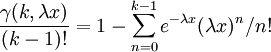\frac{\gamma(k, \lambda x)}{(k-1)!}=1-\sum_{n=0}^{k-1}e^{-\lambda x}(\lambda x)^{n}/n!
Media k/\lambda\,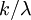
Mediana —
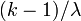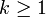
Moda (k-1)/\lambda\, for k \geq 1\,
Varianza 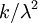k /\lambda^2\,
Coeficiente de simetría 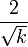\frac{2}{\sqrt{k}}
Curtosis \frac{6}{k}
Entropía 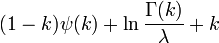(1-k)\psi(k) + \ln \frac{\Gamma(k)}{\lambda} + k
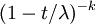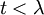
Función generadora de momentos (mgf) (1 - t/\lambda)^{-k}\, for t < \lambda\,
Función característica 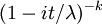(1 - it/\lambda)^{-k}\,

En estadística, la distribución Erlang, es una distribución de probabilidad continua con dos parámetros k y

λ cuya función de densidad para valores x > 0 es

f(x) = \lambda e^{-\lambda x} \frac{(\lambda x)^{k-1}}{(k-1)!}

La distribución Erlang es el equivalente de la distribución gamma con el parámetro 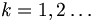k=1,2\ldots y λ = 1 / θ. Para k = 1 eso es la distribución exponencial. Se utiliza la distribución Erlang para describir el tiempo de espera hasta el suceso número k en un proceso de Poisson.

Su esperanza viene dada por: E(X) = k / λ

Su varianza viene dada por: V(X) = k / λ2

La función generadora de momento responde a la expresión: (1 − t / λ) − k

Véase también

Obtenido de "Distribuci%C3%B3n de Erlang"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Distribución de Erlang — En estadística y simulación la distribución (de) Erlang es una distribución de probabilidad continua con dos parámetros y cuya función de densidad para valores es La distribución Erlang es el equivalente de la …   Enciclopedia Universal

  • Erlang (desambiguación) — Saltar a navegación, búsqueda Erlang puede referirse a: el lenguaje de programación Erlang; Agner Krarup Erlang, el matemático, estadístico, e ingeniero danés, que dio nombre a varios conceptos: la unidad de tráfico Erlang; la distribución Erlang …   Wikipedia Español

  • Distribución gamma — Saltar a navegación, búsqueda Distribución gamma. En estadística la distribución gamma es una distribución de probabilidad continua con dos parámetros k y λ cuya función de densidad para valores …   Wikipedia Español

  • Erlang — Para otros usos de este término, véase Erlang (desambiguación). Erlang es un lenguaje de programación concurrente y un sistema de ejecución que incluye una máquina virtual y bibliotecas. El subconjunto de programación secuencial de Erlang es un… …   Wikipedia Español

  • Agner Krarup Erlang — Contenido 1 Biografía 2 Contribuciones …   Wikipedia Español

  • Distribución gamma — En estadística la distribución gamma es una distribución de probabilidad continua con dos parámetros y cuya función de densidad para valores es Aquí es el número e y es la …   Enciclopedia Universal

  • Unidad Erlang — El Erlang es una unidad adimensional utilizada en telefonía como una medida estadística del volumen de tráfico. Recibe el nombre del ingeniero danés A. K. Erlang, pionero de la teoría de colas. El tráfico de un Erlang corresponde a un recurso… …   Wikipedia Español

  • Teoría de colas — En ciencias de la computación, y más específicamente en investigación de operaciones, la teoría de colas es el estudio matemático de las líneas de espera o colas dentro de una red de comunicaciones. Su objetivo principal es el análisis de varios… …   Wikipedia Español

  • HiPE — es un compilador a código de nativo de Erlang. Sus siglas quieren decir High Performance Erlang , indicando su divergencia de las implementaciones más comúnes: emulación. HiPE es una codificación completa de Erlang, permite integración entre… …   Wikipedia Español

  • Distribuciones continuas — Saltar a navegación, búsqueda Contenido 1 Conjunto discreto 2 Tipos de Variables 3 Distribución de probabilidad para variable continua …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”