Teoría del funcional de la densidad

Teoría del funcional de la densidad

La Teoría del Funcional de la Densidad (DFT en sus siglas en inglés) es un procedimiento variacional alternativo a la solución de la ecuación de Schrödinger, en el que el parámetro a optimizar es el funcional que relaciona la distribución de densidad electrónica con la energía del sistema. Es uno de los métodos más utilizados en los cálculos cuánticos de la estructura electrónica de la materia, tanto en la física de la materia condensada como en la química cuántica.

Los orígenes de la teoría del funcional de la densidad electrónica se encuentran en un modelo desarrollado por Llewellyn Thomas y Enrico Fermi a final de los años 1920. Sin embargo, no fue hasta mediados de los años 1960 cuando las contribuciones de Pierre Hohenberg, Walter Kohn y Lu Sham establecieron el formalismo teórico en el que se basa el método usado actualmente. En 1998 Walter Kohn recibió el premio Nobel de Química por sus aportes al desarrollo de esta teoría.[1]

Los métodos tradicionales dentro de las teorías de la estructura electrónica de la materia, en particular la teoría de Hartree-Fock y los derivados de este formalismo, se basan en una función de ondas multielectrónica. Si bien esta resolución de la ecuación de Schrödinger permite describir de forma exacta el comportamiento de los sistemas muy pequeños, su capacidad de predicción se ve limitada por el hecho de que sus ecuaciones son demasiado complejas de resolver numéricamente o menos aún analíticamente. La DFT reformula el problema para ser capaz de obtener, por ejemplo, la energía y la distribución electrónica del estado fundamental, trabajando con el funcional de la densidad electrónica en vez de con la función de ondas. Una ventaja es que la densidad es una magnitud mucho más simple que la función de ondas y por lo tanto más fácil de calcular y en la práctica son accesibles sistemas mucho más complejos: la función de ondas de un sistema de N electrones depende de 3N variables, mientras que la densidad electrónica sólo depende de 3 variables. Una desventaja es que, salvo los casos más simples, no se conoce de manera exacta el funcional que relaciona esta densidad con la energía del sistema. En la práctica, se usan funcionales que se han comprobado que dan buenos resultados.

Originalmente, la DFT se desarrolló en el marco de la teoría cuántica no relativista (ecuación de Schrödinger independiente del tiempo) y de la aproximación de Born-Oppenheimer. La teoría fue extendida posteriormente al dominio de la mecánica cuántica dependiente del tiempo, y sa habla de la TD-DFT o Teoría del Funcional de la Densidad Dependiente del Tiempo y del dominio relativista. Entre otras cosas, esto permite calcular estados excitados.

Este método es uno de los exponentes máximos de la interpretación probabilística de la mecánica cuántica.

Contenido

Historia

Las leyes físicas fundamentales que son necesarias para la teoría matemática de una gran parte de la física y la totalidad de la química son pues completamente conocidas, y la dificultad es únicamente que la aplicación exacta de estas leyes lleva a ecuaciones demasiado complicadas como para ser resolubles.
Paul A.M. Dirac, 1929[2]

Las primeras nociones de una teoría del funcional de la densidad fueron desarrolladas por Thomas y Fermi en los años 1920. Calcularon la energía de un átomo, representando su energía cinética como función de su densidad electrónica, y combinando esto con las expresiones clásicas de las interacciones núcleo-electrón y electrón-electrón (que también se pueden representar en términos de densidad electrónica). El modelo fue mejorado por Dirac, que añadió un funcional de energía de intercambio en 1928. Sin embargo, la teoría de Thomas-Fermi-Dirac era imprecisa para la mayoría de las aplicaciones, por la mala representación de la energía cinética como función de la densidad.

La base teórica para la DFT fue dada en 1964 por Hohenberg y Kohn, quienes mostraron que la energía es un funcional de la densidad y que además la densidad del sistema minimiza este funcional. Sin embargo, el desarrollo más importante fue dado el año siguiente, cuando Kohn y Sham demostraron que a partir de la teoría del funcional de la densidad es posible escribir una ecuación para orbitales de una partícula, de los cuales se obtiene la densidad.

La DFT era muy popular para cálculos de física del estado sólido desde los años 1970. Sin embargo, se consideraba que no era lo bastante precisa para la química cuántica hasta los años 1990, cuando se refinaron en gran medida las aproximaciones usadas en la teoría. Ahora la DFT es un método fundamental para los cálculos de estructura electrónica en ambos campos.

Descripción de la teoría

Si no te gusta la respuesta, cambia la pregunta.
Richard M. Martin[3]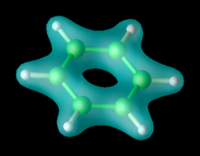
Representación de la densidad electrónica de una molécula de Benceno en el estado fundamental.

Funcionales y método variacional

El método variacional o principio variacional, basado en el cálculo de variaciones, parte de una descripción matemática de un sistema cuántico que se pueda relacionar con la energía del sistema. Por la propia definición del estado fundamental, si la descripción es lo bastante rigurosa, es posible variar los parámetros de la misma para minimizar la energía obtenida, y la función que resulte en la energía mínima será la mejor descripción del estado fundamental. En la resolución habitual de la ecuación de Schrödinger, la descripción es la función de ondas, de forma que la función de ondas que minimice la energía del sistema es la que mejor representa al estado fundamental.

La teoría del funcional de la densidad se basa en elevar la densidad electrónica desde una simple propiedad al descriptor principal del sistema.[4] De esta forma, la distribución espacial de densidad electrónica que minimice la energía será la que corresponda al estado fundamental. Un funcional es una función que recibe como argumento otra función; el funcional de la densidad es la relación entre la energía del sistema y la función espacial de la densidad electrónica; la derivada funcional depende la variación de la densidad electrónica con las coordenadas espaciales, que resulta de un único cálculo, y de la variación de la energía con la función densidad, que resulta de múltiples cálculos.[5]

Un funcional sencillo pero de utilidad práctica en el contexto de esta teoría es el llamado potencial de Hartree, que relaciona, para un parámetro de posición \vec{r}, un valor a la energía potencial \nu[n(\vec{r'})] con cada posible función de distribución de densidad electrónica n(\vec{r'}):[6]

\nu[n(\vec{r'})]=q^2 \int d^3 r' \frac{n(\vec{r'})}{|\vec{r}-\vec{r'}|}

Teorema de Khon-Sham

En la mecánica cuántica estándar, los observables son calculados a partir de la función de onda de muchos cuerpos. El método de la DFT fue sometido a un tratamiento riguroso por Hohenberg y Kohn en 1964,[7] quienes demostraron que, para el estado fundamental, existe una relación uno a uno entre la densidad y la función de onda. Esto quiere decir que la densidad electrónica en el estado fundamental contiene la misma información que la función de onda y que toda propiedad observable de un sistema electrónico puede ser calculado a partir de la densidad electrónica.[8]

En particular, Hohenberg y Kohn mostraron que la energía es un funcional de la densidad y que además la densidad del sistema minimiza este funcional. Desde el punto de vista numérico, la función de onda es un objeto muy complejo de manipular, pues para N partículas es una función de 3N variables, mientras que la densidad es más fácil de manejar pues es siempre una función de 3 variables, independientemente del número de partículas. El problema, es que no se conoce la forma completa de este funcional.

Kohn y Sham presentaron una forma de aproximar la energía cinética en 1965, mapeando el problema de la densidad a un sistema de ecuaciones monoelectrónicas. Para esto se incorpora el concepto de orbital de métodos de función de ondas, aunque estos orbitales y sus autoenergías no tienen significación física directa. La ecuación de Kohn—Sham es la ecuación de Schrödinger de un sistema ficticio de electrones que no interaccionan entre sí y que generan la misma densidad que un sistema con partículas en interacción.[9] [10] El potencial de Kohn—Sham veff(r) incluye las interacciones coulombianas (intercambio y correlación) entre los electrones y permite definir la función de ondas como el determinante de Slater construído a partir de los orbitales que dan la energía más baja para el problema de valores propios:

\left(-\frac{\hbar^2}{2m}\nabla^2+v_{\rm eff}(\mathbf r)\right)\phi_{i}(\mathbf r)=\varepsilon_{i}\phi_{i}(\mathbf r).

Las ecuaciones de Kohn—Sham se resuelven iterativamente, de forma no muy distinta al método de Hartree-Fock.

Intercambio y correlación

Aún con esta aproximación, no se conoce la forma funcional para las energías de intercambio (también llamado interacción de canje) y correlación electrónicas. Estas corresponden a la interacción cuántica entre electrones, la primera debido al principio de exclusión de Pauli entre electrones del mismo espín y el segundo debido a la parte cuántica de la repulsión coulombiana. Una solución a este problema es el desarrollo de métodos híbridos como el B3LYP,[11] [12] [13] pero existen otros métodos dentro de la propia teoría del funcional de la densidad.

La primera aproximación para este funcional se conoce como Aproximación de Densidad Local (LDA) y consiste en suponer que en cada punto, la energía de intercambio y correlación depende sólo de la densidad en ese punto. Este valor se considera como el que tendría un gas de electrones libres de esa densidad. Si bien es una aproximación bastante fuerte, se obtienen resultados sorprendentemente precisos para algunas propiedades, y es en parte a eso que se debe el éxito de esta teoría.

Existen aproximaciones más sofisticadas para el funcional de intercambio y correlación, estas se conocen como Aproximaciones de Gradiente Generalizado , estas son semilocales, ya que consideran en cada punto el valor de la densidad y sus gradientes. Para algunas propiedades estas aproximaciones dan mejores resultados que LDA, en particular para geometrías moleculares y energías del estado fundamental, aunque para otras no representan una mejora sustancial.

Una serie de funcionales más sofisticados puede obtenerse al suponer que la energía de intercambio y correlación depende explícitamente de los orbitales de Kohn-Sham. El más común de estos funcionales es el de Intercambio Exacto (EXX), que incluye de manera completa la energía de intercambio electrónico y que puede derivarse desde primeros principios. El problema de este tipo de funcionales es que computacionalmente son más costosos de tratar.

Extensiones

La teoría del funcional de la densidad ha sido generalizada para tratar sistemas más complejos. Una de las generalizaciones más importantes es la teoría del funcional de la densidad tiempo-dependiente (TDDFT por sus siglas en inglés) que permite ampliar la teoría para el estudio de sistemas bajo excitaciones.

Aplicaciones y comparación con otros métodos

Commons-emblem-question book orange.svg
 Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas.
Puedes añadirlas así o avisar al autor principal del artículo en su página de discusión pegando: {{subst:Aviso referencias|Teoría del funcional de la densidad}} ~~~~

La principal ventaja de la Teoría del Funcional de la Densidad es que las ecuaciones de esta son mucho más simples de resolver que las ecuaciones de muchos cuerpos de mecánica cuántica u otras aproximaciones, por lo que permiten tratar sistemas más grandes y calcular mas propiedades. Por lo general es posible llegar a hacer simulaciones con unos pocos miles de átomos.

El principal problema es que si bien es en principio una teoría exacta, solo se puede aplicar de forma aproximada, lo que hace que sus resultados sean menos precisos que otros métodos. Además, diferentes aproximaciones a la energía de intercambio y correlación pueden dar resultados diferentes. Aun así, para muchos métodos más sofisticados se utiliza como punto de partida los resultados de DFT.

Por este motivo, hay cierta división en la comunidad científica. Los defensores de la DFT indican que sus resultados son muy satisfactorios, y que, por su bajo coste computacional, es la única forma de abordar sistemas más allá de cierta complejidad. Sus detractores apuntan a que es un método semiempírico más, y que no es tan fiable como los métodos ab initio «clásicos».

En este sentido, existe una controversia sobre si la Teoría del Funcional de la Densidad puede ser considerada o no un método ab initio. En general en física se le considera así, debido a que no se requiere ningún tipo de parámetro adicional ni ajuste obtenido de resultados experimentales. En química por el contrario, suele guardarse el termino ab initio para métodos derivados de la teoría cuántica de muchos cuerpos que por lo general son más precisos, más costosos computacionalmente y cuyo nivel de aproximación puede ser ajustado.

Véase también

  • Anexo:Software de ayuda para DFT

Referencias y notas

  1. ↑ The Nobel Fundation (1998). «The Nobel Prize of Chemistry 1998». Consultado el 16 de junio de 2010. «The Nobel Prize in Chemistry 1998 was divided equally between Walter Kohn "for his development of the density-functional theory" and John A. Pople "for his development of computational methods in quantum chemistry".».
  2. ↑ P.A.M. Dirac (1929). «Quantum Mechanics of Many-Electron Systems» (en inglés). Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 123 (792). pp. 714-733. «The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known,and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble.». 
  3. ↑ Martin, Richard M. (2004). Cambridge University Press. ed (en inglés). Electronic Structure Basic Theory and Practical Methods. pp. 135. ISBN 0521782856. «If you don't like the answer, change the question» 
  4. ↑ La segunda sección de (Capelle, 2006), «What is density-functional theory?» pp.4-8 contiene una explicación excelente. Una frase clave: «All this is done by promoting the particle density n(r) from just one among many observables to the status of key variable, on which the calculation of all other observables can be based.»
  5. ↑ Tercera sección de (Capelle, 2006), «Functionals and their derivatives» pp.8-10.
  6. ↑ (Capelle, 2006), pág. 9
  7. ↑ P. Hohenberg y W. Kohn, Phys. Rev. 136 (1964) B864
  8. ↑ (Capelle, 2006), pág. 10; se pueden encontrar más detalles en las pp. 10-15.
  9. ↑ «Self-Consistent Equations Including Exchange and Correlation Effects». Physical Review 140 (4A):  pp. A1133–A1138. 1965. doi:10.1103/PhysRev.140.A1133. 
  10. ↑ Parr, Robert G.; Yang, Weitao (1994). Density-Functional Theory of Atoms and Molecules. ISBN 978-0195092769. 
  11. ↑ A. D. Becke, J. Chem. Phys. 38 (1998) 3089
  12. ↑ C. Lee, W. Yang, y R. G. Parr, Phys. Rev. B 37 (1988) 785
  13. ↑ P. J. Stephens, F. J. Devlin, C. F. Chabalowski, y M. J. Frisch, J. Phys. Chem. 98 (1994) 11623

Fuentes

Bibliografía adicional


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Teoría del Funcional de la Densidad — La Teoría del Funcional de la Densidad (DFT en sus siglas en inglés) es una teoría de la estructura electrónica que está escrita en términos de distribución de densidad electrónica. Esto contrasta con los métodos tradicionales en mecánica… …   Enciclopedia Universal

  • Teoría del funcional de la densidad tiempo-dependiente — La teoría del funcional de la densidad tiempo dependiente o TDDFT, es una ampliación de la Teoría del Funcional de la Densidad para tratar sistemas excitados o sistemas sometidos a la acción de potenciales tiempo dependientes. Contenido 1… …   Wikipedia Español

  • Densidad (mecánica cuántica) — Saltar a navegación, búsqueda En Mecánica cuántica las partículas no pueden ser consideradas puntuales, sino que se encuentran deslocalizadas espacialmente. La densidad (también llamada densidad de probabilidad) es una función que determina la… …   Wikipedia Español

  • Densidad (desambiguación) — Saltar a navegación, búsqueda En demografía, densidad de población se refiere a la cantidad de seres por unidad de área. En lipoproteínas, densidad puede referirse a Lipoproteína de baja densidad (LDL) y a Lipoproteína de alta densidad. En… …   Wikipedia Español

  • Teoría perturbacional — En mecánica cuántica, la teoría perturbacional o teoría de perturbaciones es un conjunto de esquemas aproximados para describir sistemas cuánticos complicados en términos de otros más sencillos. La idea es empezar con un sistema simple y… …   Wikipedia Español

  • Funcional (matemática) — En matemáticas, el término funcional se aplica a ciertas funciones. Hay dos maneras comunes en que se aplica: éstas se relacionan históricamente, pero divergen algo durante el siglo XX. Contenido 1 El significado original 2 Ecuación funcional 3… …   Wikipedia Español

  • Densidad — ► sustantivo femenino 1 Concentración de mucha materia en relación con el volumen del cuerpo que la contiene: ■ la densidad de un texto; la densidad del aceite. SINÓNIMO consistencia espesura 2 FÍSICA Relación entre la masa o peso de un cuerpo y… …   Enciclopedia Universal

  • Teoría clásica de campos — La teoría clásica de campos describe la dinámica de los fenómenos físicos macroscópicos descriptibles mediante un campo físico. Si bien potencialmente el concepto de campo engloba desde los campos de fuerzas clásicos, también la mecánica de… …   Wikipedia Español

  • Densidad espectral — Saltar a navegación, búsqueda DEP de una señal aleatoria en la banda de 0kHz 20kHz estimada mediante el método de Welch En matemáticas y en física, la Densidad Espectral (Spectral Density) de una señal es una función matemática que nos informa de …   Wikipedia Español

  • Teoría de campos — En física, la teoría de campos describe el conjunto de principios y técnicas matemáticas que permiten estudiar la dinámica y distribución espacial de los campos físicos. Así por ejemplo la teoría de campos permite describir específicamente como… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”