Fórmula de Brahmagupta

Fórmula de Brahmagupta

En geometría , la fórmula Brahmagupta encuentra el área de cualquier cuadrilátero dadas las longitudes de los lados y algunos de los ángulos. En su forma más común, se obtiene el área de los cuadriláteros que se pueda inscribir en un círculo .

Contenido

Forma Básica

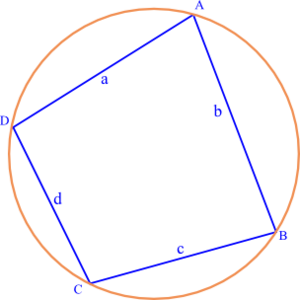
En su base y más fácil de recordar la forma, la fórmula Brahmagupta da el área de un cuadrilátero cuyos lados tienen longitudes a, b, c, d como:

A = \sqrt{(s-a)(s-b)(s-c)(s-d)}

donde s, es el semiperímetro, así:

s = \frac{a+b+c+d}{2}\cdot
s-a = \frac{-a+b+c+d}{2}
s-b = \frac{a-b+c+d}{2}
s-c = \frac{a+b-c+d}{2}
s-d = \frac{a+b+c-d}{2}

Esta fórmula generaliza la fórmula de Herón para el área de un triángulo . De hecho, la fórmula de Herón pueden derivarse de la fórmula de Brahmagupta al permitir acercarse a un valor de cero. Un triángulo puede ser considerado como un cuadrilátero con un lado de longitud cero. Desde esta perspectiva, como D tiende a cero, un cuadrilátero cíclico converge en un triángulo cíclico (todos los triángulos son cíclicos), y la fórmula de Brahmagupta converge en la fórmula de Herón.

Demostración de la fórmula de Brahmagupta

ចតុកោណចារឹកក្នុងរង្វង់.png

Si el área del cuadrilátero es A, entonces:

\begin{align} A &= \text{area} \triangle ADB + \text{area} \triangle BDC \\ &= \frac{a b \sin \widehat A}{2} + \frac{c d \sin \widehat C}{2} \end{align}

Pero desde ABCD es un cuadrilátero cíclico, D\widehat AB = 180^\circ - D\widehat CB. Por consiguiente, \sin \widehat A = \sin \widehat C. Por lo tanto

A = \frac {ab \sin \widehat A}{2} + \frac {cd \sin \widehat A}{2}
A^2 = \frac {\sin^2 \widehat A}{4} \cdot (ab + cd)^2
4A^2 = (1 - \cos^2 \widehat A)(ab + cd)^2 \,
4A^2 = (ab + cd)^2 - \cos^2 \widehat A \cdot (ab + cd)^2. \,

Aplicando el teorema del coseno para \triangle ADB y \triangle BDC e igualando las expresiones para el lado DB, tenemos

a^2 + b^2 - 2ab \cos \widehat A = c^2 + d^2 - 2cd \cos \widehat C. \,

Sustituyendo \cos \widehat C = -\cos \widehat A (ya que los ángulos son complementarios), y reordenando se obtiene:

2\cos \widehat A \cdot (ab + cd) = a^2 + b^2 - c^2 - d^2. \,

Sustituyendo esta expresión en la ecuación para el área,

4A^2 = (ab + cd)^2 - \frac {(a^2 + b^2 - c^2 - d^2)^2}{4}
16A^2 = 4(ab + cd)^2 - (a^2 + b^2 - c^2 - d^2)^2, \,

que es de la forma a2 − b2 y por lo tanto se puede escribir en la forma (a + b)(a − b) como,

(2(ab + cd) + a^2 + b^2 - c^2 - d^2)(2(ab + cd) - a^2 - b^2 + c^2 + d^2) \,
= ( (a+b)^2 - (c-d)^2 )( (c+d)^2 - (a-b)^2 ) \,
= (a+b+c-d)(a+b+d-c)(a+c+d-b)(b+c+d-a). \,

La semisuma de todos los lados es igual al semiperímetro: s = \frac{a+b+c+d}{2},

16A^2 = 16(s-a)(s-b)(s-c)(s-d). \,

Tomando la raíz cuadrada, obtenemos

A = \sqrt{(s-a)(s-b)(s-c)(s-d)}.

Extensión a los cuadriláteros no cíclicos

En el caso de los cuadriláteros cíclicos no, la fórmula de Brahmagupta puede extenderse al considerar las medidas de dos opuestos ángulos del cuadrilátero

\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\theta}

donde θ es la mitad de la suma de dos ángulos opuestos. (La pareja es irrelevante: si los otros dos ángulos se toman, la mitad de su suma es el suplemento de θ. Dado que cos(180° − θ) = −cosθ, tenemos cos2(180° − θ) = cos2θ.) Se desprende de ello que el área de un cuadrilátero cíclico es el área máxima posible para cualquier cuadrilátero con las longitudes laterales dado.

Esta fórmula general es más conocido a veces como la fórmula de Bretschneider, pero de acuerdo a MathWorld se debe aparentemente a Coolidge en esta forma, la expresión de Bretschneider es

\sqrt{(s-a)(s-b)(s-c)(s-d)-\textstyle{1\over4}(ac+bd+pq)(ac+bd-pq)}\,

donde p y q son las longitudes de las diagonales del cuadrilátero.

Es una característica de los cuadriláteros cíclicos (y en última instancia, de ángulos inscriptos) que los ángulos opuestos de un cuadrilátero suman 180°. En consecuencia, en el caso de un cuadrilátero inscrito, θ = 90 °, donde el término

abcd\cos^2\theta=abcd\cos^2 \left(90^\circ\right)=abcd\cdot0=0, \,

dando la forma básica de la fórmula de Brahmagupta.

Teoremas Relacionados

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Fórmula de Herón — Triángulo de lados a, b, c. En geometría, la fórmula de Herón, descubierta por Herón de Alejandría, relaciona el área de un triángulo en términos de las longitudes de sus lados a, b y c …   Wikipedia Español

  • Brahmagupta — (audio|Brahmagupta pronounced.ogg|listen) (598–668) was an Indian mathematician and astronomer. Life and work Brahmagupta was born in 598 CE in Bhinmal city in the state of Rajasthan of northwest India. He likely lived most of his life in… …   Wikipedia

  • Brahmagupta's formula — In geometry, Brahmagupta s formula finds the area of any quadrilateral given the lengths of the sides and some of their angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle. Basic form In its… …   Wikipedia

  • Brahmagupta — born 598 died с 665, possibly Bhillamala, Rajasthan, India Indian mathematician and astronomer. His principal work, the Brahma sphuta siddhanta ( The Opening of the Universe ), most of which deals with planetary motion, also contains important… …   Universalium

  • Brahmagupta interpolation formula — In trigonometry, the Brahmagupta interpolation formula is a special case of the Newton Stirling interpolation formula to the second order, which Brahmagupta used in 665 to interpolatenew values of the sine function from other values already… …   Wikipedia

  • Bretschneider's formula — In geometry, Bretschneider s formula is the following expression for the area of a quadrilateral,: ext{area} = sqrt {(T p)(T q)(T r)(T s) pqrs cos^2 frac{A+C}{2. Here, p , q , r and s are the sides of the quadrilateral, T is half the perimeter,… …   Wikipedia

  • Brahmagupta's formula — noun A particular expression for the area of a quadrilateral …   Wiktionary

  • Heron's formula — In geometry, Heron s (or Hero s) formula states that the area (A) of a triangle whose sides have lengths a , b , and c is :A = sqrt{sleft(s a ight)left(s b ight)left(s c ight)}where s is the semiperimeter of the triangle::s=frac{a+b+c}{2}.Heron s …   Wikipedia

  • Historia de la matemática — Página del Compendio de cálculo por el método de completado y balanceado de Muhammad ibn Mūsā al Khwārizmī (820 d.C.) La historia de las matemáticas es el área de estudio que abarca las investigaciones sobre los orígenes de los descubrimi …   Wikipedia Español

  • Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”