Fórmula de Herón

Fórmula de Herón
Triángulo de lados a, b, c.

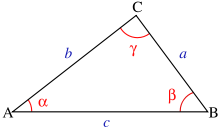
En geometría, la fórmula de Herón, descubierta por Herón de Alejandría, relaciona el área de un triángulo en términos de las longitudes de sus lados a, b y c:

\acute{A} = \sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}

donde s es el semiperímetro:

s = \frac{a+b+c}{2}

La fórmula puede reescribirse de la siguiente forma:

\acute{A} = {\ \sqrt{(a+b+c)(a+b-c)(b+c-a)(c+a-b)\,}\ \over 4}\,

Contenido

Ejemplo

Un triángulo con lados 3, 25 y 26 tiene semiperímetro (3 + 25 + 26)/2 = 27. Así, su área es \acute{A} = \sqrt{27 \cdot 24 \cdot 2 \cdot 1}=36.

Demostración

Una demostración moderna, que emplea álgebra y trigonometría (bastante distinta a la que dio Herón en su libro), podría ser la siguiente. Sea un triángulo de lados a, b, c, cuyos ángulos opuestos a cada uno de esos lados son \widehat A, \widehat B, \widehat C. Entonces, por el teorema del coseno:

\cos \widehat C = \frac{a^2+b^2-c^2}{2ab}.

De la identidad pitagórica

\sin^2 \widehat C +\cos^2 \widehat C = 1

se obtiene:

\sin \widehat C = \sqrt{1-\cos^2 \widehat C} = \frac{\sqrt{4a^2 b^2 -(a^2 +b^2 -c^2)^2 }}{2ab}.

La altura de un triángulo de base a tiene una longitud b \cdot \sin \widehat C

\begin{align} \acute{A} & = \frac{1}{2} (\mbox{base}) (\mbox{altura}) \\ & = \frac{1}{2} ab\sin \widehat C \\ & = \frac{1}{4}\sqrt{4a^2 b^2 -(a^2 +b^2 -c^2)^2} \\ & = \frac{1}{4}\sqrt{(2a b -(a^2 +b^2 -c^2))(2a b +(a^2 +b^2 -c^2))} \\ & = \frac{1}{4}\sqrt{(c^2 -(a -b)^2)((a +b)^2 -c^2)} \\ & = \frac{1}{4}\sqrt{(c -(a -b))(c +(a -b))((a +b) -c)((a +b) +c)} \\ \end{align}

Como 2s = a+b+c \,, se llega finalmente a:

\acute{A} = \sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}.

Estabilidad numérica

La fórmula de Herón dada más arriba es numéricamente inestable para triángulos de ángulos muy pequeños (como ocurre frecuentemente en astronomía). Una alternativa numéricamente más estable[1] implica reordenar las longitudes de los lados de modo que a ≥ b ≥ c, y luego realizar el computo con acuerdo total a la siguiente forma reordenada, de la fórmula de Herón:

\acute{A} = \frac{1}{4}\sqrt{(a+(b+c)) (c-(a-b)) (c+(a-b)) (a+(b-c))}.

En la fórmula precedente los paréntesis son absolutamente necesarios para evitar la inestabilidad numérica en la evaluación.

Generalizaciones

Desigualdad triangular, \{a,b,c\}\in\mathbb{R^+} .

La fórmula de Herón es un caso particular de la fórmula de Brahmagupta para el cálculo del área de cuadriláteros inscritos en una circunferencia; y ambas son casos particulares de la fórmula de Bretschneider para calcular área de un cuadrilátero.

Expresando parte de la fórmula de Herón (sólo los términos internos a la raíz) de forma matricial dentro de un determinante en términos de cuadrados de distancias de los tres vértices dados (más precisamente, el valor absoluto del determinante), obtenemos:

\acute{A}=\frac{1}{4} \sqrt{\left|{det \begin{bmatrix} 0 & a^2 & b^2 & 1 \\ a^2 & 0 & c^2 & 1 \\ b^2 & c^2 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{bmatrix}}\right|}

Donde a, b y c son las longitudes de los lados del triángulo y A será el área del mismo. Hay que asegurarse que los datos a, b y c que se proveen al determinante cumplan con la desigualdad triangular (véase figura), de lo contrario no se trataría de un triángulo y en ese caso el determinante daría resultados positivos o cero pero erróneos. Por otra parte con datos que si cumplan con la desigualdad triangular el determinante da siempre resultados negativos (no necesariamente erróneos pero inapropiados dentro de una raíz) por lo cual es necesario tomar el valor absoluto del determinante que está dentro de la raíz, de lo contrario obtendríamos resultados complejos.

Así como un triángulo está determinado por las longitudes de sus tres lados, un tetraedro lo está por las longitudes de sus seis lados. Tartaglia halló la fórmula del volumen del tetraedro en función de las longitudes de sus lados. Los determinantes de Cayley-Menger generalizan esta fórmula a dimensiones por encima de tres.

Notas y referencias

  1. ↑ W. Kahan Miscalculating Area and Angles of a Needle-like Triangle

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

Mira otros diccionarios:

  • Fórmula de Herón — En geometría, la fórmula de Herón plantea que la superficie de un triángulo de lados a, b, c viene dada por: donde p es el semiperímetro La fórmula puede ser reescrita de la siguiente forma …   Enciclopedia Universal

  • Herón de Alejandría — Herón de Alejandría. Nacimiento ca. 10 d. C. Alejandría, Egipto helenístico Fallecimiento …   Wikipedia Español

  • Fórmula de Brahmagupta — En geometría , la fórmula Brahmagupta encuentra el área de cualquier cuadrilátero dadas las longitudes de los lados y algunos de los ángulos. En su forma más común, se obtiene el área de los cuadriláteros que se pueda inscribir en un círculo .… …   Wikipedia Español

  • Heron (disambiguation) — The word heron may refer to: *Heron, the wading birds *Heron, a dinghy *De Havilland Heron, a four engine aircraft. *Heron, a folk rock band, recording on the Dawn Records label in the early 1970s *Heron Plastics, a kit car manufacturer in the… …   Wikipedia

  • Fórmula — (Del lat. formula, marco, regla.) ► sustantivo femenino 1 Regla establecida de antemano para decir o hacer una cosa: ■ terminó la carta con una fórmula de despedida. SINÓNIMO norma pauta 2 FÍSICA, MATEMÁTICAS Expresión simplificada de un cálculo… …   Enciclopedia Universal

  • formula — /fawr myeuh leuh/, n., pl. formulas, formulae / lee /. 1. a set form of words, as for stating or declaring something definitely or authoritatively, for indicating procedure to be followed, or for prescribed use on some ceremonial occasion. 2. any …   Universalium

  • Herón de Alejandría — Herón (o Hero) de Alejandría (aproximadamente año 10 dC. alrededor de los años 70) fue un ingeniero griego, floreció en Alejandría, posiblemente en el siglo primero. Después de la decadencia del Imperio Alejandrino y con él la ciencia griega,… …   Enciclopedia Universal

  • Heron's formula — Formula for finding the area of a triangle in terms of the lengths of its sides. In symbols, if a, b, and c are the lengths of the sides: Area = s(s a)(s b)(s c)where s is half the perimeter, or (a + b + c)/2. * * * …   Universalium

  • Herón, fórmula de — Fórmula para obtener el área de un triángulo en función de las longitudes de sus lados. En símbolos, si a, b, y c son las longitudes de los lados: área = s(s a)(s b)(s c) en donde s es la mitad del perímetro, es decir, (a + b + c)/2 …   Enciclopedia Universal

  • Heron's formula — In geometry, Heron s (or Hero s) formula states that the area (A) of a triangle whose sides have lengths a , b , and c is :A = sqrt{sleft(s a ight)left(s b ight)left(s c ight)}where s is the semiperimeter of the triangle::s=frac{a+b+c}{2}.Heron s …   Wikipedia

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”