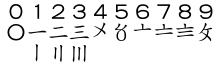Historia de la notación matemática

Este artículo o sección necesita una revisión de ortografía y gramática. Puedes colaborar editándolo (lee aquí sugerencias para mejorar tu ortografía). Cuando se haya corregido, borra este aviso por favor.

La notación matemática comprende los símbolos utilizados para escribir ecuaciones matemáticas y fórmulas. Incluye números arábigos, cartas de la época romana, griego, hebreo, alemán y alfabetos, y una serie de símbolos inventados por los matemáticos durante los últimos siglos.

El desarrollo de la notación matemática para el álgebra se puede dividir en tres etapas. La primera es "retórica", donde todos los cálculos se realizan por medio de palabras y símbolos que se utilizan. La mayoría de matemáticos islámicos medievales pertenecían a esta etapa. El segundo es "sincopado", donde con frecuencia las operaciones utilizadas y las cantidades están representadas por abreviaturas simbólica. El tercero es "simbólico", que es un sistema completo de notación y sustitución de todos los retóricos. Este sistema fue utilizado por matemáticos medievales de la India y en Europa desde mediados del siglo 17.

(Ver tabla de símbolos matemáticos para obtener una lista de símbolos.)

Al Principio

La matemática escrita comenzó con números expresados como marcas de cotejo, con cada cuenta que representan una sola unidad. Por ejemplo, una muesca en un hueso representa un animal, o persona, o cualquier otra cosa. La notación simbólica fue la de los egipcios. Tenían un símbolo de uno, diez, cien, mil, diez mil, cien mil y un millón. Dígitos pequeños fueron colocados a la izquierda del número, como en números arábigos. Más tarde, los egipcios usaron la escritura hierática en lugar de la escritura jeroglífica para mostrar los números. Hierática era más como varios grupos de cursiva y sustituye los símbolos con los individuales. Por ejemplo, las cuatro líneas verticales usadas para representar cuatro fueron reemplazados por una sola línea horizontal. El sistema que usaron los egipcios fue descubierto y modificado por muchas otras civilizaciones en el Mediterráneo. Los egipcios también tenían símbolos para las operaciones básicas, por ejemplo las piernas caminado hacia adelante representando la suma y las piernas caminando hacia atrás para representar la resta.

Al igual que los egipcios, los mesopotámicos tenían símbolos para cada potencia de diez. Más tarde, escribieron sus números en casi exactamente la misma forma que se hizo en los tiempos modernos. En lugar de tener símbolos para cada potencia de diez, que acaba de poner el coeficiente de ese número, Cada dígito fue en un principio sólo separados por un espacio, en la época de Alejandro el Grande, que había creado un símbolo que representaba al cero y fue un marcador de posición. Los mesopotámicos también utilizan un sistema sextagesimal, que es de sesenta bases. Es este sistema el que se utilizaba en los tiempos modernos en la medición de tiempo y ángulos.

Notación griega

Los griegos al principio emplearon la numeración ática, que se basaba en el sistema de los egipcios y que más tarde fue adaptada y utilizada por los romanos. Los Números del uno al cuatro fueron líneas verticales, como en los jeroglíficos. El símbolo de cinco fue el pente letra griega, que fue la primera letra de la palabra cinco. Números del seis al nueve fueron pentes con líneas verticales a su lado. El Diez estuvo representado por la primera letra de la palabra diez, Deka, uno-cien por la primera letra de la palabra cien, etc.

La numeración jónico utiliza el alfabeto entero y tres letras arcaicas.

Este sistema apareció en el siglo III a. C., antes de la digamma letras (Ϝ), Koppa (Ϟ), y Sampi (Ϡ) se convirtió en arcaico. Cuando aparecieron las letras minúsculas, estos reemplazaron a las mayúsculas como los símbolos de notación. Múltiplos de mil fueron escritos como los primeros nueve números con un golpe por delante de ellos, por lo que fue mil, α, dos mil fue, β, etc M se usa para multiplicar números de diez mil. El número 88888888 se puede escribir como H, ηωπη ηωπη * [2]

El Razonamiento matemático griego era casi en su totalidad geométrico (aunque a menudo se utiliza para razonar acerca de temas no geométricos, tales como la teoría de números), y por lo tanto, los griegos no tenían ningún interés en los símbolos algebraicos. La gran excepción fue Diofanto de Alejandría, la primera gran algebrista. Su Arithmetica fue uno de los primeros textos que utilizaban símbolos en las ecuaciones. No estaba completamente simbólico, pero fue mucho más que los libros anteriores. Un número desconocido fue llamado s. La plaza de s fue DELTA.y, el cubo se Ky, el cuarto poder se ΔyΔ, y la quinta potencia se ΔKy. La expresión 2x4 + 3x3 - 4x2 + 5x - 6 se puede escribir como SS2 C3 S4 X5 M u6.

Notación China

Los Números del 0-9 en Chino huāmǎ (花碼) numerals

Los números chinos usados que se parecen mucho al sistema de conteo. Números del uno al cuatro fueron las líneas horizontales. Cinco fue una "X" entre dos líneas horizontales, se veía casi exactamente el mismo que el número romano para diez. Hoy en día, el sistema huāmǎ sólo se utiliza para mostrar los precios en los mercados chinos o en los tradicionales facturas escritas a mano.

números árabes

A pesar de su nombre, los números arábes en realidad comenzó en la India. La razón de esto es erróneo europeos por primera vez los números utilizados en un libro en árabe, relativo al arte hindú del cálculo, por Mohommed ibn Musa al-Khwarizmi. Al-Khwarizmi no reclamó los números como el árabe, pero con varias traducciones latinas, el hecho de que los números eran indios de origen se ha perdido.

Uno de los primeros libros europeos que defendió el uso de los números fue el Liber Abaci, Leonardo de Pisa, mejor conocido como Fibonacci. Liber Abaci es más conocido por el problema matemático Fibonacci escribió en él de una población de conejos. El crecimiento de la población llegó a ser una secuencia de Fibonacci, donde un término es la suma de los dos términos anteriores.

notación del norte de África

Ibn Abu al-Hasan Ali al-Qalasādī (1412-1482) fue el último gran algebrista medieval árabe, y mejoró la notación algebraica anterior utilizada en el Magreb por Ibn al-Banna en el siglo 13 [4] y por Ibn al- Yasamin en el siglo 12. [cita requerida] En contraste con las anotaciones sincopadas de sus predecesores, Diofanto y Brahmagupta, que carecían de los símbolos de operaciones matemáticas, la notación algebraica [5] de Al-Qalasadi fue la primera en tener símbolos para estas funciones y por tanto uno de"los primeros pasos hacia la introducción del simbolismo algebraico." Representó los símbolos matemáticos utilizando caracteres del alfabeto árabe.

Pre-cálculo

Dos de los símbolos más utilizados matemáticas son la suma y la resta, + y -. El signo más se utilizó por primera vez por Nicole Oresme en proportionum Algorismus, posiblemente, una abreviatura de "et", que es "y" en América (en gran parte de la misma manera el símbolo de unión que empezó como "otros"). El signo menos se utilizó por primera vez por Johannes Widmann en Aritmética Mercantil. Widmann utilizó el signo de menos con el signo más, para indicar déficit y superávit, respectivamente. [6] El símbolo radical de la raíz cuadrada fue introducido por Christoph Rudolff porque se parecía a una minúscula "r" (de "base"). El símbolo de la constante pi, π, también fue utilizado por primera vez durante este tiempo.

En 1557 Robert Recorde publicó La piedra de afilar de Witte, que usa el signo igual (=), así como los signos más y menos para el lector Inglés. El álgebra de Nuevo (1591) de Francois Viéte introdujo la notación moderna manipulación de expresiones algebraicas. En 1631 William Oughtred presenta el signo de multiplicación (×) y sin abreviaturas y cos para las funciones trignometric.

William Jones usó π en mathesios palmariorum Sinopsis en 1706 porque es la primera letra de la palabra griega perimetron (περιμετρον), lo que significa que el perímetro en griego. Este uso fue popularizado por Euler en 1737.

Cálculo

Cálculo tenía dos principales sistemas de notación, cada uno creado por uno de los creadores: la desarrollada por Isaac Newton y la notación desarrollada por Gottfried Leibniz. Leibniz es la notación más utilizado hoy en día. Newton era simplemente un punto o un guion colocado encima de la función. Por ejemplo, la derivada de la función de x se escribiría. La segunda derivada de x se escribiría, etc En el uso moderno, esta notación designa en general a los derivados de las cantidades físicas con respecto al tiempo, y se utiliza con frecuencia en la ciencia de la mecánica.

Leibniz, en cambio, utilizó la letra "d" como un prefijo para indicar la diferenciación, e introdujo la notación que representa derivados como si fueran un tipo especial de fracción. Por ejemplo, la derivada de la función de x con respecto a la variable t en la notación de Leibniz se escribiría. Esta notación se hace explícita la variable con respecto a los cuales la derivada de la función se toma.

Leibniz también creó el símbolo de integral. El símbolo es una S alargada, lo que representa la palabra latina Summa, que significa "suma". Cuando la búsqueda de áreas bajo la curva, la integración es a menudo se ilustra mediante la división del área en un número infinito de rectángulos de altura, delgado, cuyas áreas se agregan.

Euler

Leonhard Euler fue uno de los matemáticos más prolíficos de la historia, y tal vez también fue el inventor más prolífico de la notación canónica. Sus contribuciones incluyen su uso del correo para representar a la base de los logaritmos naturales. No se sabe exactamente por qué fue elegido e, pero fue probablemente debido a que las primeras cuatro letras del alfabeto ya eran utilizados para representar las variables y constantes otros. Euler fue también uno de los primeros en utilizar π para representar pi constantemente. El uso de π se sugirió por primera vez por William Jones, quien lo utilizó como forma abreviada de perímetro. Euler fue también el primero en utilizar i para representar la raíz cuadrada de uno negativo, a pesar de que antes lo usaban como un número infinito. (Hoy en día el símbolo creado por John Wallis, se utiliza para el infinito.) Para el sumatorio, Euler fue el primero en utilizar sigma, Σ, como en. Para las funciones, Euler fue el primero en usar la notación f(x) para representar una función de x.

Peano

En 1895 Giuseppe Peano publicó la primera edición de su Formulario matemático, un esfuerzo para digerir las matemáticas en un texto breve sobre la base de símbolos especiales. El ejemplar pasó a Bertrand Russell en 1900 en una conferencia de París tan impresionado Russell que él también fue tomada con la unidad para hacer las matemáticas más concisa. El resultado fue escrita Principia Mathematica con Alfred North Whitehead. Este tratado marca un hito en la literatura moderna, donde se convirtió en símbolo dominante. Formulario de Peano Mathematico, aunque menos popular que el trabajo de Russell, continuó a través de cinco ediciones. El quinto apareció en 1908 e incluyó 4.200 fórmulas y teoremas.

Lógica

Una vez que la lógica fue reconocida como una parte importante de las matemáticas, que recibió su propia notación. Algunos de los primeros fue el conjunto de símbolos utilizados en el álgebra de Boole, creada por George Boole en 1854. Boole mismo no veía la lógica como una rama de las matemáticas, pero ha llegado a ser abarcado todos modos. Símbolos que se encuentran en el álgebra de Boole incluyen (Y), (O), y (NO). Con estos símbolos y letras para representar diferentes valores verdad, uno puede hacer declaraciones lógicas tales como, que es "(uno es verdadero o un NO es cierto) es cierto", lo que significa que es cierto que es verdadero o no verdadero ( es decir falso). álgebra de Boole tiene muchas aplicaciones prácticas como es, pero también fue el comienzo de lo que sería un gran conjunto de símbolos utilizados en la lógica. La mayoría de estos símbolos se pueden encontrar en el cálculo proposicional, un sistema formal de lo descrito. Α es el conjunto de elementos, tales como la a en el ejemplo anterior con el álgebra de Boole. Ω es el conjunto que contiene los subconjuntos que contienen las operaciones, tales como productos o componentes. Ζ contiene las reglas de inferencia, que son los que dictan las normas como las inferencias pueden ser lógicamente hecho, y Ι contiene los axiomas. (Véase también: Básico y Derivados argumento formas). Con estos símbolos, las pruebas se puede decir que son completamente artificiales.

Mientras que prueba su teoremas de la incompletitud, Kurt Gödel creado una alternativa a los símbolos utilizados normalmente en la lógica. Él usó los números de Gödel, que eran los números que representan las operaciones con los números de conjunto, y las variables con los primeros números primos mayores de 10. Con números de Gödel, las declaraciones de la lógica se puede descomponer en una secuencia de números. Gödel a continuación, dio un paso más, teniendo los primeros n números primos y su puesta a la potencia de los números en la secuencia. Estos números se multiplicaron luego juntos para obtener el producto final, dando a cada declaración de la lógica de su propio número. [7] Por ejemplo, tome la declaración "No existe un número x tal que no es y". Uso de los símbolos del cálculo proposicional, esto llegaría a ser. Si los números de Gödel reemplazar los símbolos, se convierte en {8, 4, 11, 9, 8, 11, 5, 1, 13, 9}. Hay diez números, así que los diez primeros números primos se encuentran y son {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}. A continuación, los números de Gödel se hacen los poderes de los números primos respectiva y se multiplicaron, dando. El número resultante es aproximadamente.