Ley del paralelogramo

Ley del paralelogramo
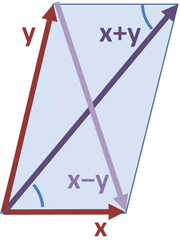
Un paralelogramo. Los lados de éste están mostrados en color azul y las diagonales en rojo.

En matemática, la forma más simple de la ley del paralelogramo pertenece a la geometría elemental. Ésta postula que la suma de los cuadrados de las longitudes de los cuatro lados de un paralelogramo es igual a la suma de los cuadrados de las longitudes de las dos diagonales de éste. Utilizando la notación del paralelogramo mostrado en la figura de la derecha, se puede escribir matemáticamente como:

(AB)^2+(BC)^2+(CD)^2+(DA)^2=(AC)^2+(BD)^2.\,

En el caso de que el paralelogramo sea un rectángulo, las dos diagonales son iguales y la ley se reduce al teorema de Pitágoras. Pero en general, no se cumple que el cuadrado de una diagonal sea igual a la suma de los cuadrados de dos lados.

Contenido

Ley del paralelogramo para espacios con producto interno

Vectores involucrados en la ley del paralelogramo.

En espacios provistos de producto escalar, la definición de la ley del paralelogramo se reduce a la identidad algebraica

2\|x\|^2+2\|y\|^2=\|x+y\|^2+\|x-y\|^2

donde

\|x\|^2=\langle x, x\rangle.\,

es el producto escalar normado.

Espacios vectoriales normados que satisfacen la ley del paralelogramo

La mayoría de espacios vectoriales normados reales y complejos no poseen producto interno, pero todos los espacios vectoriales normados tienen norma (por definición), y por lo tanto se puede evaluar las expresiones a ambos lados del "=" en la identidad anterior. Un hecho notable es que si la identidad anterior se mantiene, entonces la norma debe surgir de la manera habitual de algún producto interno. Además, el producto interno que se genera mediante la norma es único, como consecuencia de la identidad de polarización, en el caso real, éste viene dado por dada por

\langle x, y\rangle={\|x+y\|^2-\|x-y\|^2\over 4},\,

o, equivalentemente, por

{\|x+y\|^2-\|x\|^2-\|y\|^2\over 2} \ \ \rm{\acute{o}} \ \ {\|x\|^2+\|y\|^2-\|x-y\|^2\over 2}.\,

En el caso complejo, éste es dado por

\langle x, y\rangle={\|x+y\|^2-\|x-y\|^2\over 4}+i{\|ix-y\|^2-\|ix+y\|^2\over 4}.

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Paralelogramo — Saltar a navegación, búsqueda Los cuatro tipos de paralelogramo. En el sentido de las agujas del reloj: cuadrado, rombo, romboide y rectángulo. El cuadrado y el rectángulo son paralelogramos rectángulos, mientras que los otros dos son… …   Wikipedia Español

  • Teorema del coseno — El teorema del coseno es una generalización del teorema de Pitágoras en los triángulos no rectángulos que se utiliza, normalmente, en trigonometría. El teorema relaciona un lado de un triángulo con los otros dos y con el coseno del ángulo formado …   Wikipedia Español

  • Teorema de Apolonio — fig.1: Esquema con áreas → ( ). En geometría, el teorema de Apolonio, también llamado teorema de la mediana, es un teorema que relaciona …   Wikipedia Español

  • Ecuación funcional — Saltar a navegación, búsqueda En matemáticas o en sus aplicaciones, una ecuación funcional es una ecuación que se expresa a través de una combinación de variables independientes y funciones incógnitas, cuya expresión y valor deben ser resueltos.… …   Wikipedia Español

  • Mediana (geometría) — Las medianas de un triángulo (líneas rojas) se cortan en el baricentro del mismo. En geometría las transversales de gravedad.</ref> de un triángulo son, cada uno de los tres segmentos de recta, que unen cada vértice con el punto medio de su …   Wikipedia Español

  • Espacio prehilbertiano — Saltar a navegación, búsqueda En matemáticas, un espacio prehilbertiano o espacio prehilbert es un espacio vectorial provisto de un producto escalar. Más concretamente, es un par , donde es un espacio vectorial sobre un cuerpo y …   Wikipedia Español

  • fuerzas concurrentes — fpl Fuerzas cuyas lнneas de acciуn tienen un punto en comъn; con la aplicaciуn de la ley del paralelogramo se puede calcular su suma vectorial …   Diccionario de Construcción y Arquitectur

  • operaciones vectoriales — Extensión de las leyes del álgebra elemental a los vectores. Comprenden adición, sustracción y tres tipos de multiplicación. La suma de dos vectores es un tercer vector, representado como la diagonal del paralelogramo construido con los dos… …   Enciclopedia Universal

  • Fuente Álamo de Murcia — Escudo …   Wikipedia Español

  • Fundación de Puebla — Representación pictórica de la fundación de Puebla. fray Toribio de Benavente (Motolinia) y Hernando de Helgueta dirigen los trabajos de la traza de la ciudad. La Fundación de Puebla que originalmente se llamó el pueblo de Los Ángeles, poco… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”