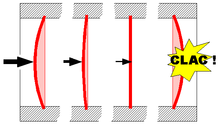
Resorte

Para otros usos de este término, véase Resorte (desambiguación).

Muelles de tracción.

Se conoce como resorte o muelle a un operador elástico capaz de almacenar energía y desprenderse de ella sin sufrir deformación permanente cuando cesan las fuerzas o la tensión a las que es sometido. Son fabricados con materiales muy diversos, tales como acero al carbono, acero inoxidable, acero al cromo-silicio, cromo-vanadio, bronces, plástico, entre otros, que presentan propiedades elásticas y con una gran diversidad de formas y dimensiones.

Se les emplean en una gran cantidad de aplicaciones, desde cables de conexión hasta disquetes, productos de uso cotidiano, herramientas especiales o suspensiones de vehículos. Su propósito, con frecuencia, se adapta a las situaciones en las que se requiere aplicar una fuerza y que esta sea retornada en forma de energía. Siempre están diseñados para ofrecer resistencia o amortiguar las solicitaciones externas.

Tipos de resortes

Resorte de torsión.

De acuerdo a las fuerzas o tensiones que puedan soportar, se distinguen tres tipos principales de resortes:

Resortes de tracción: Estos resortes soportan exclusivamente fuerzas de tracción y se caracterizan por tener un gancho en cada uno de sus extremos, de diferentes estilos: inglés, alemán, catalán, murciano, giratorio, abierto, cerrado o de dobles espira. Estos ganchos permiten montar los resortes de tracción en todas las posiciones imaginables.

Resorte cónico de compresión.

Resortes de compresión: Estos resortes están especialmente diseñados para soportar fuerzas de compresión. Pueden ser cilíndricos, cónicos, bicónicos, de paso fijo o cambiante.

Resortes de torsión: Son los resortes sometidos a fuerzas de torsión (momentos).

Existen muelles que pueden operar tanto a tracción como a compresión. También existen una gran cantidad de resortes que no tienen la forma de muelle habitual; quizás la forma más conocida sea la arandela grower.

Resorte especial.

Física del resorte

Energía de deformación

La manera más sencilla de analizar un resorte físicamente es mediante su modelo ideal global y bajo la suposición de que éste obedece la Ley de Hooke. Se establece así la ecuación del resorte, donde se relaciona la fuerza F ejercida sobre el mismo con el alargamiento/contracción o elongación x producida, del siguiente modo:

$F = -kx\,$ , siendo $k = \frac{AE}{L}$

Donde k es la constante elástica del resorte, x la elongación (alargamiento producido), A la sección del cilindro imaginario que envuelve al muelle y E el módulo de elasticidad del muelle (no confundir con el módulo de elasticidad del material).

La energía de deformación o energía potencial elástica $U k$ asociada al estiramiento o acortamiento del muelle viene dada por la integración de trabajo realizado en cada cambio infiniesimal $dx\,$ de su longitud:

$U_k = \int_{0}^{x} F(x) \ d x = \int_{0}^{x} k(x) \, x \ d x \$

Si la rigidez del muelle es independiente de su deformación, entonces

$U_k = \int_{0}^{x} kx \ dx = \frac{1}{2} kx^2$

Ecuación diferencial y ecuación de ondas

Definiremos ahora una constante intrínseca del resorte independiente de la longitud de este y estableceremos así la ley diferencial constitutiva de un muelle. Multiplicando $k$ por la longitud total, y llamando al producto $k i$ o k intrínseca, se tiene:

$k_i=AE\,$ donde $k=\frac{k_i}{L}$

Llamaremos $F(x)\,$ a la tensión en una sección del muelle situada a una distancia $x\,$ de uno de sus extremos, que consideraremos fijo y que tomaremos como origen de coordenadas, $k Δ x$ a la constante de un pequeño trozo de muelle de longitud $\Delta x\,$ a la misma distancia y $\delta_{\Delta x}\,$ al alargamiento de ese pequeño trozo en virtud de la aplicación de la fuerza $F(x)\,$ . Por la ley del muelle completo:

$F(x)=-k_{\Delta x}\delta_{\Delta x}=k_i\frac{\delta_{\Delta x}}{\Delta x}$

Tomando el límite:

$F(x)=-k_i\frac{{\delta}_{dx}}{dx}$

que por el principio de superposición resulta:

$F\left(x\right)=-k_i\frac{d{\delta}}{dx}=-AE\frac{d\delta}{dx}$

Si además suponemos que tanto la sección como el módulo de elasticidad pueden variar con la distancia al origen, la ecuación queda:

$F\left(x\right)=-k_i\left(x\right)\frac{d{\delta}}{dx}=-A\left(x\right)E\left(x\right)\frac{d\delta}{dx}$

Que es la ecuación diferencial completa del muelle. Si se integra para todo x, de obtiene como resultado el valor del alargamiento unitario total. Normalmente puede considerarse F (x) constante e igual a la fuerza total aplicada. Cuando F (x) no es constante y se incluye en el razonamiento la inercia de éste, se llega a la ecuación de onda unidimensional que describe los fenómenos ondulatorios.

Supongamos, por simplicidad, que tanto la sección del resorte, como su densidad (entendiendo densidad como la masa de un tramo de muelle dividida por el volumen del cilindro imaginario envolvente) y su módulo de elasticidad son constantes a lo largo del mismo y que el resorte es cilíndrico. Llamemos $\Psi\left(x\right)$ al desplazamiento de una sección de muelle. Ahora tomemos un tramo diferencial de muelle de longitud (dx). La masa de esa porción vendrá dada por:

$d m = ρ A d x$

Aplicando la segunda ley de Newton a ese tramo:

$F\left(x\right)-F(x+dx)\left(x\right)=-dm\frac{{\partial}^2\Psi}{{\partial t}^2}=-\rho Adx\frac{{\partial}^2\Psi}{{\partial t}^2}$

Es decir:

$\frac{\partial F}{\partial x}dx=-\rho Adx\frac{{\partial}^2\Psi}{{\partial t}^2}\rightarrow \frac{\partial F}{\partial x}=-\rho A\frac{{\partial}^2\Psi}{{\partial t}^2}$

Por otro lado es sencillo deducir que

$d\delta=\Psi\left(x+dx\right)-\Psi\left(x\right)=\frac{\partial \Psi}{\partial x}dx$

Al introducir, por tanto, esta expresión en la ecuación diferencial del muelle antes deducida, se llega a:

$F\left(x\right)=-AE\frac{\partial\Psi}{\partial d}$

Derivando esta expresión respecto a x se obtiene:

$\frac{\partial F}{\partial x}=-AE\frac{{\partial}^2\Psi}{{\partial x}^2}$

Juntando la expresión temporal con la expresión espacial se deduce finalmente la ecuación general de un muelle cilíndrico de sección, densidad y elasticidad constantes, que coincide exactamente con la ecuación de onda longitudinale:

$\frac{{\partial}^2\Psi\left(x,t\right)}{{\partial t}^2}=\frac{E}{\rho}\times\frac{{\partial}^2\Psi\left(x,t\right)}{{\partial x}^2}$

De la que se deduce la velocidad de propagación de perturbaciones en un muelle ideal como:

$c=\sqrt{\frac{E}{\rho}}$

Muelle con una masa suspendida

Para el caso de un muelle con una masa suspendida,

$\displaystyle F = -kx \ \to \ m\frac{d^2x}{dt^2}=-kx$

Cuya solución es $x = C sin ω t$ , es decir, la masa realiza un movimiento armónico simple de amplitud $C$ y frecuencia angular $ω$ . Derivando y sustituyendo:

$\ \displaystyle -\omega ^2 \cdot C \sin \omega t = -\frac{k}{m}\cdot C sin\omega t$

Simplificando:

$\displaystyle \omega = \sqrt{\frac{k}{m}}$

Esta ecuación relaciona la frecuencia natural con la rigidez del muelle y la masa suspendida.

Muelle de densidad variable

Para un muelle de densidad variable, módulo de elasticidad variable y sección de la envolvente variable, la ecuación generalizada de las perturbaciones es la que sigue:

$\frac{{\partial}^2\Psi\left(x,t\right)}{{\partial t}^2}=\frac{1}{\rho \left(x\right)}\left[\frac{\partial A\left(x\right)}{\partial x}\frac{E\left(x\right)}{A\left(x\right)}+\frac{\partial E\left(x\right)}{\partial x}\right]\frac{\partial\Psi\left(x,t\right)}{\partial x}+\frac{E\left(x\right)}{\rho \left(x\right)}\frac{{\partial}^2\Psi\left(x,t\right)}{{\partial x}^2}$

En un resorte de estas características, la onda viajera cambiaría su velocidad y, por tanto, su longitud de onda a lo largo del recorrido. Además, en unas zonas del muelle su amplitud sería mayor que en otras.

En el análisis de un resorte real, aparecen también ondas longitudinales, transversales y de torsión lo largo y ancho de las espira que se propagan a una velocidad que depende de la raíz cuadrada del módulo de elasticidad E del material para las longitudinales del módulo de elasticidad transversal G del material para las transversales y del módulo de torsión de la espira para las de torsión, divididas todas por la densidad del material.

Soluciones a la ecuación de ondas en un muelle

La solución general a la ecuación en derivadas parciales del muelle simplificado de longitud infinita se describe a continuación. Dadas las condiciones iniciales:

$\Psi(x,0)=f(x) \,$

${\Psi}_t(x,0)=g(x) \,$

donde ${\Psi}_t=\frac{\partial \Psi}{\partial t} \,$ , la función de D'Alembert solución a la ecuación de onda puede escribirse como:

Solución a condiciones iniciales senoidales.

$\Psi(x,t) = \frac{f(x-ct) + f(x+ct)}{2} + \frac{1}{2c} \int_{x-ct}^{x+ct} g(s) ds$

Tal solución admite que F y G puedan ser cualquier clase de funciones continuas $\scriptstyle f(x) \in C^k$ y $\scriptstyle g(x) \in C^{k-1}$ cuando $\scriptstyle u(t,x) \in C^k$ .

Para un muelle de longitud finita L con sus extremos anclados, el problema se convierte en uno de contorno que puede resolverse mediante separación de variables con la teoría de Sturm-Liouville. Dadas unas condiciones iniciales como las anteriormente descritas y unas condiciones de contorno de extremos fijos. Las condiciones iniciales pueden desarrollarse en una serie de Fourier de la siguiente forma:

$f\left(x\right)=\sum_{n = 1}^{\infty} A_n\sin{\left(\frac{n\pi x}{L}\right)}$

$g\left(x\right)=\sum_{n = 1}^{\infty} B_n\frac{cn\pi}{L}\sin{\left(\frac{n\pi x}{L}\right)}$

En donde los coeficientes de Fourier se obtienen tras integrar las funciones f y g como sigue:

$A_n=\frac{2}{L}\int_0^{L}f\left(x\right)\sin{\left(\frac{n\pi x}{L}\right)}dx$

$B_n=\frac{2}{n\pi c}\int_0^{L}g\left(x\right)\sin{\left(\frac{n\pi x}{L}\right)}dx$

para $n = 1,2,...$

La solución a este problema queda escrita como sigue:

$\Psi(x,t) = \sum_{n = 1}^{\infty}A_n\sin{\left(\frac{n\pi x}{L}\right)}\cos{\left(\frac{cn\pi t}{L}\right)}+\sum_{n = 1}^{\infty}B_n\sin{\left(\frac{n\pi x}{L}\right)}\cos{\left(\frac{cn\pi t}{L}\right)}$

Una onda estacionaria. Los puntos rojos representan los nodos

Véase también

Ley de elasticidad de Hooke.
Módulo de elasticidad.

Enlaces externos

Wikimedia Commons alberga contenido multimedia sobre resortesCommons.
Institute of Spring Technology.
Spring Manufacturers Institute.

Categorías:

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Sinónimos:

muelle, fleje, ballesta, espiral, tensor / influencia, enchufe, recurso, tecla, amistad, mano

Mira otros diccionarios:

resorte — sustantivo masculino 1. Área: mecánica Pieza elástica, generalmente en espiral, que puede soportar grandes deformaciones y recuperar de nuevo su posición y forma inicial: Este reloj tiene una cuerda antigua de resorte. Sinónimo: muelle. 2. Medio… … Diccionario Salamanca de la Lengua Española
Resorte — Allgemeine Informationen Genre(s) Heavy Metal, Latin Rock Gründung 1995 Website www.reb … Deutsch Wikipedia
resorte — (Del fr. ressort). 1. m. muelle (ǁ pieza elástica). 2. Fuerza elástica de algo. 3. Medio material o inmaterial de que alguien se vale para lograr un fin … Diccionario de la lengua española
Resorte — Infobox musical artist Name = Resorte Img capt = Img size = 250 Landscape = yes Background = group or band Alias = Origin = Baja California, MEX Genre = Nu metal Alternative metal Rapcore Years active = 1995–present Label = Koolarrow Records… … Wikipedia
resorte — (Del fr. ressort.) ► sustantivo masculino 1 Pieza elástica, por lo general de metal, doblada en espiral que recobra su posición inicial tras ser comprimida por una fuerza externa: ■ el resorte se quedó encallado. SINÓNIMO muelle 2 Medio o… … Enciclopedia Universal
resorte — s m 1 Pieza elástica, generalmente de metal y de forma espiral, que tiene la propiedad de volver rápidamente a su forma original cuando se deja de ejercer sobre ella alguna fuerza, de recuperarla con mayor o menor lentitud dependiendo de la que… … Español en México
resorte — {{＃}}{{LM R34014}}{{〓}} {{SynR34853}} {{［}}resorte{{］}} ‹re·sor·te› {{《}}▍ s.m.{{》}} {{＜}}1{{＞}} Pieza elástica, generalmente metálica, que se comprime y deforma cuando se aplica una presión sobre ella y que, cuando desaparece dicha presión,… … Diccionario de uso del español actual con sinónimos y antónimos
resorte — (m) (Intermedio) objeto flexible que tiene forma espiral y habitualmente constituye una parte de cosas más complejas Ejemplos: En su puño había una navaja de resorte. Dentro del colchón hay varios resortes. Sinónimos: dispositivo, espiral, muelle … Español Extremo Basic and Intermediate
Resorte (banda) — Saltar a navegación, búsqueda Resorte Información personal Origen Baja California, … Wikipedia Español
Resorte (desambiguación) — Saltar a navegación, búsqueda Resorte puede referirse a: un resorte o muelle, un objeto elástico que almacena energía al ser sometido a un esfuerzo y se despredende de ella sin deformarse cuando el esfuerzo concluye; Resorte, grupo musical… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Resorte

Contenido

Tipos de resortes