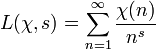Carácter de Dirichlet

Carácter de Dirichlet

Carácter de Dirichlet

En teoría de números, los caracteres de Dirichlet son un cierto tipo de funciones aritméticas que derivan de caracteres completamente multiplicativos sobre las unidades 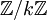\mathbb Z / k \mathbb Z . Los caracteres de Dirichlet son usados para definir las Funciones L de Dirichlet, las cuales son funciones meromorfas, con una variedad interesante de propiedades analíticas. Si χ es un caracter de Dirichlet, se define su serie L de Dirichlet de la siguiente manera:

L(\chi,s) = \sum_{n=1}^\infty \frac{\chi(n)}{n^s}

donde s es un número complejo con la parte real > 1. Por continuación analítica, esta función puede ser extendida a una función meromorfa en todo el plano complejo. Las funciones L de Dirichlet son generalizaciones de la función zeta de Riemann y aparecen en la hipótesis generalizada de Riemann.

Los caracteres de Dirichlet son llamados así en honor a Johann Peter Gustav Lejeune Dirichlet.

Definición axiomática

Un carácter de Dirichlet es cualquier función χ de números enteros a números complejos con las siguientes propiedades:

  1. Existe un entero positivo k tal que χ(n) = χ(n + k) para todo n.
  2. Si mcd (n,k) > 1 entonces χ(n) = 0; si mcd(n,k) = 1 entonces χ(n) ≠ 0.
  3. χ(mn) = χ(m)χ(n) para todo los enteros m y n.


Véase también

Obtenido de "Car%C3%A1cter de Dirichlet"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Teorema de Dirichlet — Este artículo o sección tiene un estilo difícil de entender para los lectores interesados en el tema. Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan a… …   Wikipedia Español

  • Función L de Dirichlet — En matemáticas , se llama serie L de Dirichlet, en honor a Johann Peter Gustav Lejeune Dirichlet, a una función de la forma Donde χ es un carácter de Dirichlet y s una variable compleja cuya componente real es mayor que 1. Por medio de una… …   Wikipedia Español

  • Serie de Dirichlet — En matemáticas, una serie de Dirichlet es toda serie del tipo donde s y an, n = 1, 2, 3, ... son números complejos. Las series de Dirichlet juegan un número importante de roles en la teoría analítica de números. La definición más popularizada de… …   Wikipedia Español

  • Hipótesis generalizada de Riemann — La hipótesis de Riemann es una de las conjeturas más importantes de la matemáticas. Es un postulado sobre los ceros de la función zeta de Riemann. Existen varios objetos geométricos y aritméticos que pueden ser descritos por las llamadas… …   Wikipedia Español

  • Función generadora — En matemáticas, una función generadora o función generatriz es una serie formal de potencias cuyos coeficientes codifican información sobre una sucesión an cuyo índice corre sobre los enteros no negativos. Hay varios tipos de funciones… …   Wikipedia Español

  • Producto de Euler — Saltar a navegación, búsqueda Leonhard Euler. En matemática, un producto de Euler es la expansión de un producto infinito, indexado por números primos p de una serie de Dirichlet. El nombre surge del caso especial de la función …   Wikipedia Español

  • Fórmula de Perron — En matemática, y más precisamente en teoría analítica de números, la fórmula de Perron es una fórmula dada por Oskar Perron para calcular la suma de una función aritmética, mediante el uso de una transformada de Mellin inversa. Contenido 1… …   Wikipedia Español

  • Función zeta de Dedekind — En matemática, la función zeta de Dedekind es una serie de Dirichlet definida para todo cuerpo K de números algebraicos, expresada como ζK(s) donde s es una variable compleja. Es la suma infinita: realizada sobre todos los I ideales del anillo de …   Wikipedia Español

  • Cero de Siegel — Saltar a navegación, búsqueda En matemáticas, mas específico en el campo de Teoría analítica de números, un cero de Siegel, en honor a Carl Ludwig Siegel, es un tipo de contraejemplo potencial de la hipótesis de Riemann generalizada, sobre los… …   Wikipedia Español

  • Función L — La teoría de las funciones L se ha convertido en una parte muy substancial, y todavía con numerosas conjeturas, de la teoría de números contemporánea. En ella, se construyen amplias generalizaciones de la función zeta de Riemann y de las series L …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”