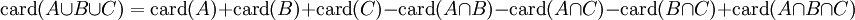- Cardinal de una unión de conjuntos
-
Cardinal de una unión de conjuntos
Sean los conjuntos:
y conociendo el cardinal de cada conjunto:
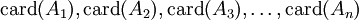 ,
,
así como el cardinal de cada intersección de dos, tres, ..., n conjuntos:
se quiere calcular Cardinal de una unión de conjuntos:
En ciertos lugares del planeta, esta fórmula se conoce bajo el nombre de fórmula de la criba. La vamos a ver generalizando a partir de la unión de dos, de tres y de n conjuntos.
Unión de dos conjuntos
Sean A y B dos conjuntos, de intersección
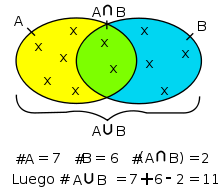
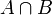 (en verde en la figura). Para contar todos los elementos de la unión
(en verde en la figura). Para contar todos los elementos de la unión 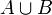 , primero contamos los de A (en amarillo y verde en la figura), luego los de B (en azul y verde) y sumamos los dos números. Pero ¡los elementos de la intersección han sido contados dos veces!
, primero contamos los de A (en amarillo y verde en la figura), luego los de B (en azul y verde) y sumamos los dos números. Pero ¡los elementos de la intersección han sido contados dos veces!Entonces tenemos que restar a la suma el cardinal de la intersección:
La fórmula es por lo tanto:
Se puede remplazar el cardinal por otra medida de conjuntos, por ejemplo por una probabilidad, si A y B son eventos probabilísticos:
donde:
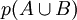 : es la probabilidad de que se dé A ó B.
: es la probabilidad de que se dé A ó B.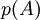 : es la probabilidad de que se dé A.
: es la probabilidad de que se dé A.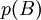 : es la probabilidad de que se dé B.
: es la probabilidad de que se dé B.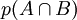 : es la probabilidad de que se dé A y B simultáneamente.
: es la probabilidad de que se dé A y B simultáneamente.
Unión de tres conjuntos
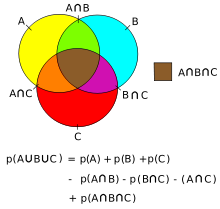
Consideremos ahora tercer conjuntos A, B y C, que interseca entre si. Para calcular la cardinal de una unión de estos tres conjuntos, tenemos:
por la propiedad asociativa de la unión, y resulta que:
que es lo mismo que:
Calculando por separado tenemos:
como en el caso de la unión de dos conjuntos, y por otro lado:
que es lo mismo que:
con estos resultados parciales, ya tenemos el resultado final:
Esto es:
Unión de n conjuntos
Fórmula general, con los conjuntos A1, A2, A3... An:
![\begin{matrix}{ } \\ \# \cup A_i \\ { }_{i \in [1;n]} \end{matrix} = \sum \# A_i - \sum_{i \ne j} \#(A_i \cap A_j) + \sum_{i \ne j \ne k \ne i} \#(A_i \cap A_j \cap A_k) - ...](/pictures/eswiki/53/52021bc986ae61e0dd6b076eaa318e86.png)
Una escritura más rigurosa pero menos legible es: ![\begin{matrix} { } \\ \# \cup A_i \\ { }_{i \in [1;n]} \end{matrix} = \sum_{k=1}^n (-1)^{k+1} \begin{matrix} { } \\ { } \\ \# \cap A_i \\ { }_{i \in I \subseteq [1;n]} \\ { }_{\# I = k} \end{matrix}](/pictures/eswiki/56/87bd45fb98476f534641babcf284519f.png)
Prueba
Se puede demostrar esta fórmula por inducción sobre el número de conjuntos involucrados. Para dos y tres es cierta por construcción; también lo es para uno y cero conjunto si se mira atentamente (recordando que la suma de ningún elemento es el neutro de la adición, en este caso el conjunto vacío).
Supongamos la fórmula cierta para n conjuntos, (A1, A2, A3... An) y añadamos uno más en la unión: An+1.Sea A la unión de los conjuntos A1, A2... An, y B el conjunto An+1 y apliquemos la fórmula para # (A U B):
![\#(A \cup B) = \# A + \# B - \# (A \cap B) = \sum_{k=1}^n (-1)^{k+1} \begin{matrix} { } \\ { } \\ \# \cap A_i \\ { }_{i \in I \subseteq [1;n]} \\ { }_{\# I = k} \end{matrix} + \# A_{n+1} - \sum_{k=1}^n (-1)^{k+1} \begin{matrix} { } \\ { } \\ \# \cap A_i \\ { }_{i \in I \subseteq [1;n]} \\ { }_{\# I = k} \end{matrix} \cap A_{n+1}](/pictures/eswiki/100/dc607723c5fc02410ba21d018e3f3b3f.png)
El #An+1 se podrá incluir en la primera suma pues corresponde al caso k = 1 y I = {n+1}.
La última suma se reescribe:
![- \sum_{k=1}^n (-1)^{k+1} \begin{matrix} { } \\ { } \\ \# \cap A_i \cap A_{n+1} \\ { }_{i \in I \subseteq [1;n]} \\ { }_{\# I = k} \end{matrix} =
+ \sum_{k=1}^n (-1)^{k+2} \begin{matrix} { } \\ { } \\ \# \cap A_i \\ { }_{i \in I' \subseteq [1;n+1]} \\ { }_{\# I = k+1} \end{matrix}](/pictures/eswiki/52/437b3ee8359454e1e914e1de2f124283.png)
con I' = I U {n+1} en la suma. Luego cambiamos de variable: k' = k + 1 y la suma anterior se escribe:
![\sum_{k'=2}^{n+1} (-1)^{k'+1} \begin{matrix} { } \\ { } \\ \# \cap A_i \\ { }_{i \in I' \subseteq [1;n+1]} \\ { }_{\# I = k'} \end{matrix}](/pictures/eswiki/100/d437609a8bc483f4162c32b6ef5cba5f.png)
Reuniendo todo lo anterior, cambiando k' por k: ![\sum_{k=1}^{n+1} (-1)^{k+1} \begin{matrix} { } \\ { } \\ \# \cap A_i \\ { }_{i \in I \subseteq [1;n+1]} \\ { }_{\# I = k} \end{matrix}](/pictures/eswiki/57/9116857eac72929ad46d50d9ee682448.png)
Esto corresponde a la fórmula para n+1, lo que acaba la inducción.
Categoría: Teoría de conjuntos
Wikimedia foundation. 2010.

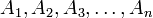
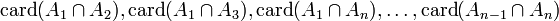
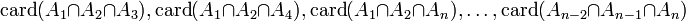
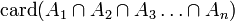
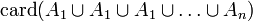
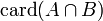
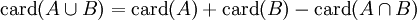
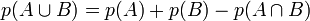
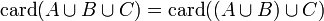
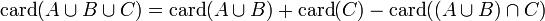
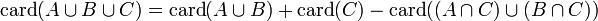
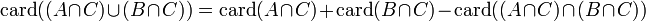
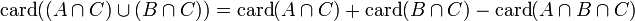
![\mbox{card}(A \cup B \cup C) = \mbox{card}(A) + \mbox{card}(B) - \mbox{card}(A \cap B) + \mbox{card}(C) -[ \mbox{card}(A \cap C) + \mbox{card}(B \cap C) - \mbox{card}(A \cap B \cap C)]](/pictures/eswiki/52/4134cf9a98d179c1f7df0c454c6738ad.png)