Circunferencia de los nueve puntos

Se conoce como circunferencia de los nueve puntos a la circunferencia asociada a cada triángulo. Su nombre deriva del hecho que la circunferencia pasa por nueve puntos notables, seis de ellos sobre el mismo triángulo (salvo que el triángulo sea obtusángulo). Estos son:

• el punto medio de cada lado del triángulo,
• los pies de las alturas, y
• los puntos medios de los segmentos determinados por el ortocentro y los vértices del triángulo.

Al círculo de los nueve puntos se le conoce también entre otros como círculo de Feuerbach, círculo de Euler, círculo de los seis puntos o círculo medioinscrito.

Historia

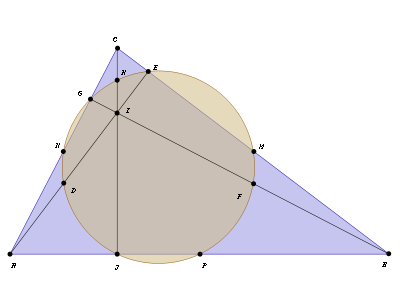
Generalmente,^[1] se adjudica a Karl Wilhelm Feuerbach el descubrimiento de la circunferencia de los nueve puntos; sin embargo, lo que Feuerbach descubrió fue la circunferencia de los seis puntos, reconociendo que sobre ella se encuentran los puntos medios de los lados de un triángulo y los pies de las alturas del triángulo (en la figura, los puntos: M N P y E G J).

Anteriormente, Charles Brianchon y Jean-Victor Poncelet habían demostrado su existencia. Poco tiempo después de Feuerbach, Olry Terquem también demostró la existencia del círculo y reconoció además que los puntos medios de los segmentos determinados por los vértices del triángulo y el ortocentro, también están contenidos en la circunferencia (en la figura, los puntos: D F H).

Demostración

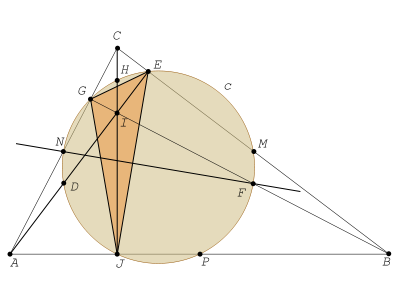
Consideremos las alturas del triángulo ABC: AE, BG y CJ (véase la figura). El triángulo GEJ es el triángulo órtico del triángulo ABC, y el punto I es el ortocentro del triángulo ABC. Las alturas de este, son las bisectrices de los ángulos internos de aquel. Los lados del triángulo ABC son las bisectrices exteriores del triángulo GEJ.

Las bisectrices del ángulo JGE cortan a la mediatriz del lado opuesto, EJ en los puntos F y N que se hallan sobre la circunferencia circunscrita c (descrito en el artículo de la bisectriz de un angulo).

Observemos que los triángulos ACJ y ACE son rectángulos teniendo ambos al lado AC como hipotenusa. Se sigue que los cuatro puntos A, C, E y J son concíclicos y el centro de la circunferencia que los contiene se halla sobre la intersección de la hipotenusa AC con la mediatriz del segmento EJ, esto es, el punto N. Se sigue que N es punto medio del segmento AC.

De modo semejante, los triángulos EIB y JIB son rectángulos compartiendo la hipotenusa IB. Por lo tanto, los puntos E, I, J y B son concíclicos y el centro de la circunferencia que los contiene se halla sobre la intersección de la hipotenusa IB con la mediatriz del segmento EJ, esto es el punto F. De igual modo, se demuestra que los puntos M y P son los puntos medios de los lados AB y BC respectivamente. De forma análoga, se demuestra que los puntos D y H son puntos medios de los segmentos AI y CI respectivamente.

Circunferencia circunscrita y de Feuerbach

Por la observación de que los puntos D, F y H satisfacen

se deduce que:

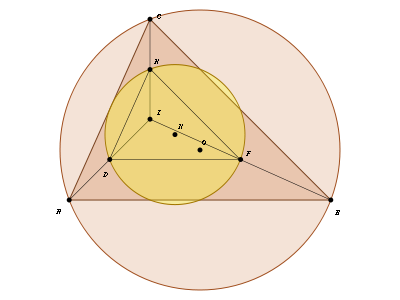
• la circunferencia de Feuerbach de un triángulo es homotética a la circunferencia circunscrita,
• el centro de la homotecia es el ortocentro del triángulo,
• la razón de la homotecia es 2.

El triángulo formado por los puntos D, F y H^[2] es semejante al triángulo ABC. También se observa que el centro de la circunferencia de Feuerbach N, es punto medio del segmento IO, donde O es el circuncentro del triángulo ABC.

Finalmente, el centro de la circunferencia de Feuerbach se halla sobre la recta de Euler del triángulo.

Otras propiedades

En 1822, Karl Feuerbach descubrió una de las propiedades más profundas sobre la circunferencia que lleva su nombre: la circunferencia de los nueve puntos es tangente exterior a los círculos exinscritos al triángulo. La circunferencia inscrita al triángulo es tangente interior a la circunferencia de Feuerbach.

La demostración de este hecho^[3] puede hacerse, observando que los puntos de tangencia de dos de las circunferencias exinscritas a uno de los lads del triángulo equidistan del punto medio de dicho lado. Usando la inversión respecto de este punto medio se le puede dar el toque final a la demostración.

Notas

1. ↑ Historia traducida de la versión en inglés del artículo.
2. ↑ Estos puntos son los llamados puntos de Euler y el triángulo determinado por ellos, el triángulo de Euler.
3. ↑ Véase Bogomolny, Alexander. «Feuerbach's Theorem: a Proof» (en inglés). Interactive Mathematics Miscellany and Puzzles.

Enlaces externos

• Weisstein, Eric W. «Nine-Point Circle» (en inglés). MathWorld. Wolfram Research.