- Conjugado (matemática)
-
En matemáticas, el conjugado de un número complejo se obtiene cambiando el signo de su componente imaginaria. Por lo tanto, el conjugado de un número complejo
(donde a y b son números reales) es
El conjugado es a menudo indicado como z * . Aquí, se utiliza la notación
 para evitar confusiones con la notación utilizada para indicar la transpuesta conjugada de una matriz (que puede pensarse como una generalización del conjugado de un número). Notar que si el número complejo es tratado como una matriz
para evitar confusiones con la notación utilizada para indicar la transpuesta conjugada de una matriz (que puede pensarse como una generalización del conjugado de un número). Notar que si el número complejo es tratado como una matriz  , las notaciones son idénticas.
, las notaciones son idénticas.Por ejemplo,
Los números complejos pueden ser representados como puntos en un plano con un sistema de coordenadas cartesianas. El eje x contiene los números reales y el eje y contiene los múltiplos de i (la unidad imaginaria). Por lo tanto, en esta representación el conjugado de un número corresponde a su reflexión sobre el eje x.
Sin embargo, en forma polar, el conjugado de reiφ queda determinado por re − iϕ. Lo cual se puede verificar fácilmente aplicando la fórmula de Euler.
Los pares formados por un número y su conjugado son importantes ya que la unidad imaginaria i es indistinta de su inversa aditiva y multiplicativa − i, ya que ambas satisfacen la definición de la unidad imaginaria: x2 = − 1. Lo más común es que, si un número complejo es solución de un problema, también su conjugado lo es, esto se verifica por ejemplo en las soluciones complejas de la fórmula cuadrática con coeficientes reales.
Propiedades
Estas propiedades se aplican a todos los números complejos z y w, a menos que se indique lo contrario.
 si w es distinto de cero
si w es distinto de cero
 si y solo si z es real
si y solo si z es real
 para todo entero n
para todo entero n
 si z es distinto de cero
si z es distinto de cero
Esta última fórmula es el método normalmente utilizado para encontrar el inverso de un número complejo si el número está expresado en coordenadas rectangulares.
 si z es distinto de cero
si z es distinto de cero
Véase también
- Espacio vectorial de conjugados
Categoría:- Números complejos
Wikimedia foundation. 2010.

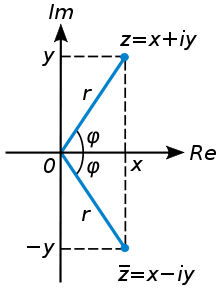
 en el plano complejo.
en el plano complejo.









