- Formulación matemática de la mecánica cuántica
-
Formulación matemática de la mecánica cuántica
La formulación matemática rigurosa de la mecánica cuántica fue desarrollada por Paul Adrien Maurice Dirac y John von Neumann. Dicha formulación canónica se basa en un conjunto de media docena de postulados (dependiendo de la formulaciones). Este artículo presenta una enumeración más o menos canónica de dichos postulados fundamentales.
Contenido
Postulado I
Todo estado cuántico está representado por una función vectorial normalizada, llamado en algunos casos "vector de estado", que debe cumplir las propiedades del producto escalar en el espacio de Hilbert complejo y separable ξ (espacios compacto con estructura vectorial y de funciones). Fijada una base del espacio de Hilbert unitaria
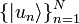 tal que,[1]
tal que,[1]se puede representar el estado de las siguientes formas vectoriales:
- Forma ket:
- Forma bra:
donde la "*" significa complejo conjugado.
El estado cuántico normalizado debe cumplir:
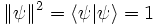 . La elección del estado normalizado no es única ya que
. La elección del estado normalizado no es única ya que 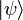 y
y 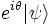 representan el mismo estado ya que la medida de cualquier magnitud en ellos es idéntica.
representan el mismo estado ya que la medida de cualquier magnitud en ellos es idéntica.Postulado II
Los observables de un sistema están representados por operadores lineales hermíticos (autoadjuntos). El conjunto de autovalores (valores propios) del observable
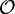 recibe el nombre de espectro y sus autovectores (vectores propios), exactos o aproximados, definen una base en el espacio de Hilbert.
recibe el nombre de espectro y sus autovectores (vectores propios), exactos o aproximados, definen una base en el espacio de Hilbert.En la misma base unitaria
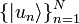 , los representantes de un observable
, los representantes de un observable 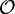 se definen como:
se definen como:En dimensión finita, los autovalores λi se encuentran diagonalizando el representante del operador: igualando a cero el siguiente determinante:
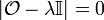 y los autovectores resolviendo el siguiente sistema de n ecuaciones:
y los autovectores resolviendo el siguiente sistema de n ecuaciones: 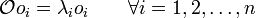
En la práctica, el espacio de Hilbert de la mayoría de sistemas reales es de dimensión infinita y el cálculo de autovalores y autovectores es un problema matemático un poco más complicado que el que debe hacerse en dimensión finita.
Postulado III
Cuando un sistema está en el estado
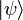 , la medida de un observable A dará como resultado el valor propio a, con una probabilidad
, la medida de un observable A dará como resultado el valor propio a, con una probabilidad 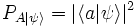 , donde
, donde 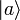 es el vector propio asociado al autovalor a (en notación del espacio de Hilbert esto se expresa como
es el vector propio asociado al autovalor a (en notación del espacio de Hilbert esto se expresa como 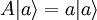 ).
).Como consecuencia de este postulado el valor esperado será:
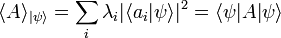
Llamaremos dispersión o incertidumbre a la raíz cuadrada de la varianza. Ésta se calcula así:
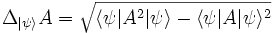
Principio de incertidumbre
El producto de las dispersiones de dos observables sobre el mismo estado está acotado.
![\Delta A \Delta B \ge \frac{1}{2} \langle \psi | [A,B]| \psi \rangle](/pictures/eswiki/50/2466b21549649ec3e82c669833db6a3a.png)
Para el caso de los observables típicos de posición (X) y momento (Px) tenemos:
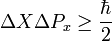
Esto es porque las variables X y Px son canónicas conjugadas, es decir que el conmutador
![[X,P_x]=i \hbar](/pictures/eswiki/100/d3b1693e6c86b1624086024ea9c6bbcf.png) .
.Postulado IV
Para cualquier estado
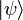 sobre el cual se hace una medida de A que filtra al estado
sobre el cual se hace una medida de A que filtra al estado 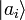 , pasa a encontrarse precisamente en ese estado
, pasa a encontrarse precisamente en ese estado 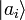 , si no se ha destruido durante el proceso.
, si no se ha destruido durante el proceso.Éste es el postulado más conflictivo de la mecánica cuántica ya que supone el colapso instantáneo de nuestro conocimiento sobre el sistema al hacer una medida filtrante.
Postulado V
La evolución temporal de un sistema se rige por la ecuación de Schrödinger:
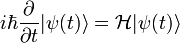
Donde H es el operador de Hamilton o hamiltoniano del sistema, que corresponde a la energía del sistema.
Postulado VI
Los operadores de posición y momento satisfacen las siguientes reglas de conmutación:
![[X_i,X_j]=0 \qquad [P_i,P_j]=0 \qquad [X_i,P_j]=i\hbar \delta_{ij}\mathbb{I}](/pictures/eswiki/97/a5b085c96a0cfd593cc1153bc4bd5ff8.png)
Nomenclatura usada
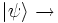 Estado cuántico
Estado cuántico
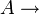 Observable
Observable
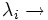 Autovalor
Autovalor
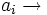 Autovector
Autovector
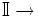 Matriz identidad
Matriz identidad
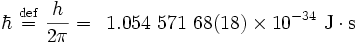 Constante reducida de Planck (h-barra)
Constante reducida de Planck (h-barra)
![[A,B] = AB - BA \rightarrow](/pictures/eswiki/98/b8b01dfdb1b73c80b8fa9bb1a78b1499.png) Conmutador
ConmutadorVéase también
- Mecánica cuántica
- Espacio de Hilbert, Hamiltoniano (mecánica cuántica).
- Observable, Espectro de un operador.
Referencias
- ↑ Cohen-Tannoudji, Claude; Bernard Diu, Franck Laloë (1977). Quantum Mechanics, vol.1, 3ª edición, París, Francia: Hermann, pp. 898. ISBN 0-471-16432-1.
Categorías: Mecánica cuántica | Axiomas de la física
Wikimedia foundation. 2010.

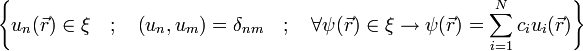
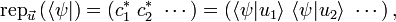
![\text{rep}_{\vec{u}}\mathcal{O}=\left[\begin{array}{ccc}
o_{11} & \dots & o_{1n} \\
\vdots & o_{ij} & \vdots \\
o_{n1} & \dots & o_{nn} \\
\end{array}\right] = \left[\begin{array}{ccc}
<u_1|\mathcal{O}|u_1> & \dots & <u_1|\mathcal{O}|u_n> \\
\vdots & <u_i|\mathcal{O}|u_j> & \vdots \\
<u_n|\mathcal{O}|u_1> & \dots & <u_n|\mathcal{O}|u_n> \\
\end{array}\right]](/pictures/eswiki/57/91e32d14368af04058884b33f5f223b4.png)