Tronco de cono

Tronco de cono
Tronco de cono.
Tronco de cono.

El tronco de cono, cono truncado o tronco de Garófalo es un volumen de revolución generado por un trapecio rectángulo al tomar como eje de giro el lado perpendicular a las bases.

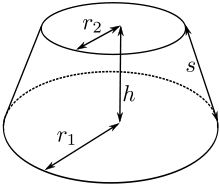
Un tronco de cono recto, de bases paralelas, es la porción de cono comprendido entre dos planos que lo cortan y son perpendiculares a su eje. Queda determinado por los radios de las bases, r_1 \, y r_2 \,, la altura, h \,, y la generatriz, s \,, entre las cuales se cumple la relación del teorema de Pitágoras:

s^2 = \left(r_1 - r_2 \right)^2 + h^2

El área lateral de un tronco de cono se puede hallar mediante la semisuma de los perímetros de las bases, por la generatriz:

A_L = \frac {2 \pi r_1 + 2 \pi r_2 }{2} s
A_L = \pi \left(r_1 + r_2 \right)s

El área de un tronco de cono, la cual es el área lateral más el área de las bases superior e inferior, se puede hallar mediante la fórmula:

A = A_1 + A_2 + A_L \,
A = \pi r_1^2 + \pi r_2^2 + \pi \left(r_1 + r_2 \right) s
A = \pi \left[ r_1^2 + r_2^2 + (r_1 + r_2 \right) s ]

El volumen de un tronco de cono se puede hallar utilizando el producto entre la altura del tronco y la media heroniana del área de las bases:

V = \frac{h}{3} \left(A_1 + A_2 + \sqrt {A_1 A_2}\right) \,
V = \frac{h}{3} \left(\pi r_1^2 + \pi r_2^2 + \sqrt { \pi r_1^2 \pi r_2^2}\right) \,
V = \frac{h \pi}{3} (r_1^2 + r_2^2 + r_1 r_2) \,

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Tronco (geometría) — tronco Ejemplos: Un tronco pentagonal y otro cuadrado Caras n trapezoides, 2 polígonos Aristas …   Wikipedia Español

  • tronco (1) — {{hw}}{{tronco (1)}{{/hw}}agg.  (pl. m. chi ) 1 Mozzo: piramide tronca. 2 (ling.) Detto di parola che ha subito troncamento | Detto di parola accentata sull ultima sillaba. 3 (fig.) Interrotto, lasciato a metà: discorso tronco | (est.) Spezzato… …   Enciclopedia di italiano

  • Tronco — (Del lat. truncus.) ► sustantivo masculino 1 BOTÁNICA Tallo principal, fuerte y macizo de los árboles y arbustos: ■ el tronco de las secuoyas es muy grande. 2 ANATOMÍA Cuerpo humano o de un animal sin la cabeza ni las extremidades: ■ el ejercicio …   Enciclopedia Universal

  • Cono (geometría) — Para otros usos de este término, véase cono. En geometría, un cono recto es un sólido de revolución generado por el giro de un triángulo rectángulo alrededor de uno de sus catetos. Al círculo conformado por el otro cateto se denomina base y al… …   Wikipedia Español

  • Cono — (Del lat. conus < gr. konos, cono, piña.) ► sustantivo masculino 1 GEOMETRÍA Cuerpo geométrico limitado por una superficie cónica, cuya directriz es una circunferencia, y por un plano, que forma su base, y que la corta. 2 GEOMETRÍA Superficie… …   Enciclopedia Universal

  • Tronco — La palabra tronco puede referirse a: Tronco (botánica) Tronco (anatomía) como parte del cuerpo humano aplícase también a los animales Torso, con el significado de tronco, en lenguaje no anatómico. En geometría se llama tronco a un cuerpo truncado …   Wikipedia Español

  • tronco — 1trón·co s.m. 1. FO fusto eretto e legnoso degli alberi e degli arbusti da cui si dipartono i rami: il tronco di un castagno, di un faggio, dell abete; segare, tagliare un tronco 2. BU fig., ceppo, stirpe: famiglie dello stesso tronco 3. TS arch …   Dizionario italiano

  • Conicidad — Tronco de cono Un cono puede cons …   Wikipedia Español

  • Generatriz — La generatriz[1] es una línea que a causa de su movimiento conforma una figura geométrica, que a su vez depende de la directriz. La generatriz puede ser una línea recta o curva.[2] Si la generatriz es una línea recta que gira respecto de otra… …   Wikipedia Español

  • Torno — Este artículo se refiere a los tornos utilizados en la industria metalúrgica para el mecanizado de metales. Para otros tipos de tornos y para otras acepciones de esta palabra, véase Torno (desambiguación) Torno paralelo moderno. Se denomina torno …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”