Espacio vectorial normado
- Espacio vectorial normado
-
Espacio vectorial normado
En matemática un espacio vectorial se dice que es normado si en él se puede definir una norma vectorial. Podemos señalar los siguientes hechos que ayudan a comprender la importancia del concepto de espacio normado:
Definición
Un espacio vectorial V sobre un cuerpo 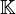 en el que se define un valor absoluto (generalmente
en el que se define un valor absoluto (generalmente  o
o 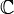 ) se dice que es normado si en él se puede definir una norma, es decir, una aplicación
) se dice que es normado si en él se puede definir una norma, es decir, una aplicación 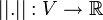 , que verifica:
, que verifica:
- No negatividad. Para todo
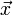 de
de 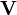 su norma ha de ser positiva, y será cero si y sólo si
su norma ha de ser positiva, y será cero si y sólo si 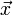 es el vector cero:
es el vector cero: 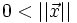 si
si 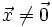 y
y 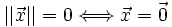 .
.
- Homogeneidad. Para todo
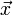 de
de 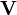 y para todo k de
y para todo k de 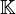 se satisface que
se satisface que 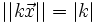 ·
· 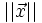 donde | | es el módulo o valor absoluto.
donde | | es el módulo o valor absoluto.
- Desigualdad triangular. Para todos
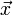 e
e 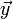 de
de 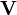 se cumple que
se cumple que 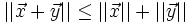 .
.
Generalmente se denotará a (V, | | ) al espacio vectorial normado y cuando la norma sea clara simplemente por V.
Ejemplos
De dimensión finita
De dimensión infinita
Distancia inducida
En todo espacio vectorial normado se puede definir la distancia 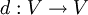 :
:
- d(x,y): = | | x − y | |
con la cual (V,d) es un espacio métrico.
Espacios vectoriales normados de dimensión finita
Se cumplen los siguientes resultados (que generalmente no son ciertos para espacios de dimensión infinita):
- Todas las normas definidas en el espacio son equivalentes, es decir, definen la misma topología. La convergencia o divergencia de una sucesión no depende de la norma escogida. El resultado no es cierto para espacios de dimensión infinita siendo siempre posible encontrar dos normas que no son equivalentes.
- El espacio es completo, es decir, es un espacio de Banach. Como consecuencia, todo subespacio de dimensión finita de un espacio vectorial (no necesariamente de dimensión finita) es cerrado.
- Un espacio vectorial normado es de dimensión finita si y sólo si la bola unidad es compacta.
- Todo funcional lineal es continuo. Si el espacio tiene dimensión infinita, existen funcionales lineales no continuos.
- Teorema de Heine-Borel o teorema de Borel-Lebesgue. Un subconjunto del espacio vectorial es compacto si y solo si es cerrado y acotado.
Categorías: Vectores | Álgebra lineal
Wikimedia foundation.
2010.
Mira otros diccionarios:
Espacio vectorial — Saltar a navegación, búsqueda Un espacio vectorial es un conjunto de objetos (llamados vectores) que pueden escalarse y sumarse. Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra… … Wikipedia Español
Espacio — Saltar a navegación, búsqueda Espacio (del latín spatium) se refiere: Especialmente al espacio físico, en el que se ubican los objetos sensibles; y la extensión que contiene toda la materia existente; la distancia entre dos cuerpos; la distancia… … Wikipedia Español
Espacio euclídeo — Saltar a navegación, búsqueda El espacio euclídeo o euclidiano es el espacio matemático n dimensional usual, una generalización de los espacios de 2 (plano euclídeo) y 3 dimensiones estudiados por Euclides. Estructuralmente un espacio euclídeo es … Wikipedia Español
Espacio de Banach — Saltar a navegación, búsqueda En matemáticas, los espacios de Banach, llamados así en honor de Stefan Banach, son uno de los objetos de estudio más importantes en análisis funcional. Los espacios de Banach son típicamente espacios de funciones de … Wikipedia Español
Espacio completo — Saltar a navegación, búsqueda En análisis funcional un espacio métrico X se dice que es completo si toda sucesión de Cauchy converge, es decir, existe un elemento del espacio que es el límite de la sucesión. La idea intuitiva de este concepto es… … Wikipedia Español
Espacio de Sóbolev — Saltar a navegación, búsqueda Un espacio de Sóbolev es un tipo de espacio vectorial funcional, dotado de una norma de tipo Lp, tal que la función y sus derivadas hasta cierto orden tienen norma finita. Un espacio de Sóbolev puede ser considerado… … Wikipedia Español
Espacio métrico — Saltar a navegación, búsqueda En matemática, un espacio métrico es un tipo particular de espacio topológico donde una distancia entre puntos está definida. Corresponde al caso muy común en que se dispone de una noción de distancia sobre el… … Wikipedia Español
Espacio dual — En matemáticas, la existencia de un espacio vectorial dual refleja de una manera abstracta la relación entre los vectores fila (1×n) y los vectores columna (n×1). La construcción puede darse también para los espacios infinito dimensionales y da… … Wikipedia Español
Espacio euclídeo — Un espacio euclideo es un espacio vectorial normado de dimensión finita en que la norma es heredada de un producto escalar. El espacio euclídeo es el espacio matemático n dimensional usual , una generalización de los espacios de 2 y 3 dimensiones … Enciclopedia Universal
Espacio — (Del lat. spatium, campo para correr.) ► sustantivo masculino 1 Extensión o superficie en que está contenida la materia. 2 Parte de esta extensión que ocupa un cuerpo: ■ necesito un piso más grande y con más espacio. SINÓNIMO sitio 3 Distancia… … Enciclopedia Universal
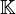 en el que se define un valor absoluto (generalmente
en el que se define un valor absoluto (generalmente  o
o 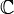 ) se dice que es normado si en él se puede definir una norma, es decir, una aplicación
) se dice que es normado si en él se puede definir una norma, es decir, una aplicación 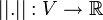 , que verifica:
, que verifica: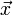 de
de 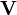 su norma ha de ser positiva, y será cero si y sólo si
su norma ha de ser positiva, y será cero si y sólo si 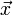 es el vector cero:
es el vector cero: 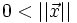 si
si 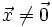 y
y 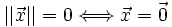 .
.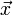 de
de 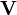 y para todo k de
y para todo k de 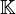 se satisface que
se satisface que 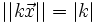 ·
· 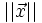 donde | | es el módulo o valor absoluto.
donde | | es el módulo o valor absoluto.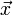 e
e 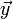 de
de 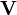 se cumple que
se cumple que 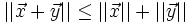 .
.
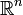 .
. :
: 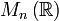
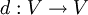 :
: