Curva del dragón

Curva del dragón

Curva del dragón

Proceso de formación de este fractal.

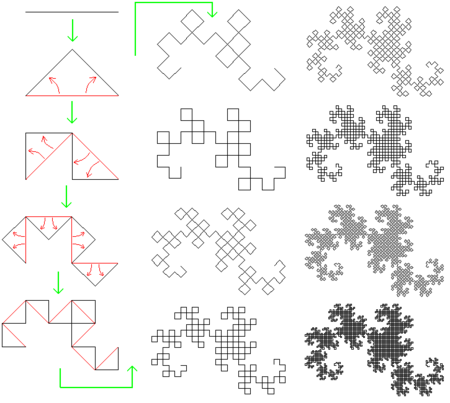
La curva del dragón es un fractal que se construye siguiendo los siguientes pasos:

  • A partir de un segmento, se construye el triángulo rectángulo e isósceles, como lo muestra las dos primeras figuras. Luego se borra el segmento inicial.
  • Se repite un sinfín de veces el proceso de remplazar un segmento por otros dos para cada línea de la curva, alternando siempre la orientación de los triángulos.

La siguiente figura muestra los trece primeros pasos:

formación de la curva del dragón

Agrandando la imagen y después de una veintena de iteraciones, se obtiene la curva del dragón:

curva del dragón

Como se puede observar, esta curva llega a rellenar completamente una parte del plano, por lo que su dimensión fractal debe ser 2. El cálculo de su dimensión se hace como en el copo de nieve de Koch, pués las construcciones de ambas curvas son similares.
Si uno se fija en el primer paso de la construcción, se observa que a partir del segmento inicial se obtienen los otros catetos del primer triángulo mediante dos similitudes (una es indirecta) de razón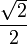 \frac {\sqrt{2}} 2, de centros los extremos del segmento, y de ángulos 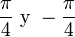\frac {\pi} 4 \mbox{ y } -\frac {\pi} 4 radianes (o sea 45º). Llamemos s1 y s2 éstas dos similitudes. Por construcción misma, la enésima figura obtenida en el proceso, Dn, es la reunión de las imágenes por s1 y s2 de la figura anterior Dn-1:

Dn = s1(Dn-1) ∪ s2(Dn-1)


Tomando el límite de ésta relación ( n tiende hacia + ∞), y llamando D = D∞ la curva del dragón, obtenemos:

D = s1(D) ∪ s2(D)

.

Es decir que D es la reunión de dos copias de si misma, a escala 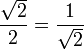\frac {\sqrt{2}} 2 = \frac 1 \sqrt{2} , como se puede ver en la figura siguiente:

homotecias internas del dragón

Por tanto si agrandamos D con una homotecia de razón

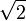
\sqrt 2

, obtenemos dos veces D, a la misma escala. Si D es de dimensión d, su "volumen" es multiplicado por

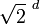
{\sqrt 2}^{ \ d}

por esta homotecia. Aquí tenemos pues:

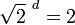
{\sqrt 2}^{ \ d} = 2

y por tanto d = 2.

Y para rematar, una sorprendente propiedad de la curva del dragón: Se puede pavimentar el plano con ella, es decir rellenarlo sin dejar huecos y sin que se sobrepongan dos o más "piezas":

pavimento del plano con dragones

Referencias

Enlaces externos

El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.
Obtenido de "Curva del drag%C3%B3n"

Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Curva del dragón — La curva del dragón es un fractal que se puede construir así: ● A partir de un segmento, se construye el triángulo rectángulo e isósceles, como lo muestra las dos primeras figuras. Luego se borra el segmento inicial. ● Se repite un sinfín de… …   Enciclopedia Universal

  • Kung Fu del Dragón — Los movimientos del estilo del Dragón (chino: 龍形摩橋, pinyin: lóng xíng mó qiáo; Yale Cantonese: lung4 ying4 mo1 kiu4; literalmente forma de dragón que araña puentes ) de la artes marciales de China están basados en el mítico Dragón Chino.… …   Wikipedia Español

  • Curva de Gosper — La curva de Gosper, nombrada así en honor a Bill Gosper, es una curva de Peano. Es un fractal similar en su construcción a la curva del dragón o a la de Hilbert. Cuarta iteración de la curva de Gosper. La línea que una el punto rojo con el …   Wikipedia Español

  • Spyro: Year of the Dragon — Desarrolladora(s) Insomniac Games Universal Interactive Studios Distribuido …   Wikipedia Español

  • Guerra del Anillo — Para el libro editado por Christopher Tolkien, véase La Guerra del Anillo. Guerra del Anillo El Anillo Único con su inscripción en lengua negra …   Wikipedia Español

  • Gran Camino del Este — En el universo imaginario del escritor J. R. R. Tolkien y en las novelas El hobbit y El Señor de los Anillos, el Gran Camino del Este es la ruta más importante de Eriador que lo cruza todo de oeste a este y continua, luego de atravesar las… …   Wikipedia Español

  • Baby (personaje de Dragon Ball) — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Historia del arte — Para la historiografía de la historia del arte, véase Estudio de la historia del arte. La creación …   Wikipedia Español

  • Historia del desnudo artístico — David (1501 1504), de Miguel Ángel, Galería de la Academia de Florencia. La evolución histórica del desnudo artístico ha corrido en paralelo a la historia del arte en general, salvo pequeñas particularidades derivadas de la distinta aceptación de …   Wikipedia Español

  • Fractal — Este artículo o sección sobre matemáticas necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 16 de octubre de 2010. También puedes… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”