- Esponja de Menger
-
Esponja de Menger
En matemáticas, la esponja de Menger es un conjunto fractal descrito por primera vez en 1926 por Karl Menger[1] mientras exploraba el concepto de dimensión topológica.[2]
Al igual que la alfombra de Sierpinski constituye una generalización bidimensional del conjunto de Cantor, esta es una generalización tridimensional de ambos. Comparte con estos muchas de sus propiedades, siendo un conjunto compacto, no numerable y de medida de Lebesgue nula. Su dimensión dimensión fractal de Hausdorff es
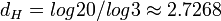
Es de destacar su propiedad de curva universal, pues es un conjunto topológico de dimensión topológica uno, y cualquier otra curva o grafo es homeomorfo a un subconjunto de la esponja de Menger.
Construcción
La construcción de la esponja de Menger se define de forma recursiva:
- Comenzamos con un cubo (primera imagen).
- Dividimos cada cara del cubo en 9 cuadrados. Esto subdivide el cubo en 27 cubos más pequeños, como le sucede al cubo de Rubik.
- Eliminamos los cubos centrales de cada cara (6) y el cubo central (1), dejando sólamente 20 cubos (segunda imagen).
- Repetimos los pasos 1, 2 y 3 para cada uno de los cubos menores resultantes.
La esponja de Menger es el límite de este proceso tras un número infinito de iteraciones.
Véase también
Referencias
- ↑ Karl Menger, General Spaces and Cartesian Spaces, (1926) Communications to the Amsterdam Academy of Sciences. English translation reprinted in Classics on Fractals, Gerald A.Edgar, editor, Addison-Wesley (1993) ISBN 0-201-58701-7
- ↑ Karl Menger, Dimensionstheorie, (1928) B.G Teubner Publishers, Leipzig.
Categorías: Fractales | Curvas | Espacio topológico
Wikimedia foundation. 2010.


