Función de Weierstrass

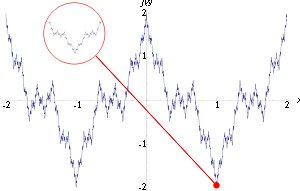Función de Weierstrass
Función de Weierstrass en el intervalo [−2, 2]. La función tiene un comportamiento fractal.

La función de Weierstrass es muy particular. Su nombre, por supuesto es por su mentor, quien la publicó por primera vez, Karl Weierstrass. Está definida en la recta y toma valores reales. Lo que la hace particular es que es continua en todo punto y no es derivable o diferenciable en ninguno.

La función de Weierstrass fue la primera conocida con esta propiedad. De este modo, Weierstrass mostró que era falsa la conjetura que circulaba en aquella época que afirmaba que las funciones continuas eran diferenciables salvo en puntos aislados.

La función, tal como la definió Weierstrass, es la siguiente

f(x)=\sum_{n=0}^\infty a^n\cos(b^n\pi x),

donde 0 < a < 1, b es un entero impar y positivo y cumplen que

ab > 1+\frac{3}{2} \pi.

La prueba de que la función es continua es sencilla. Dado que las sumas parciales son continuas y que la serie es uniformemente convergente, se deduce que el límite es continuo.

Otra propiedad interesante de esta función es su condición fractal. Si bien su gráfico no es rigurosamente autosemejante (véase ampliación en el gráfico, arriba), la dimensión del mismo gráfico no es uno ni dos. De hecho la dimensión de Hausdorff está acotada inferiormente por \frac{\log a}{\log b +2} y se cree que ese sea su valor (eso es lo que se prueba en el libro de Falconer).

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Función gamma — en el eje real. Valor absoluto de la función gamma en el plano complejo …   Wikipedia Español

  • Función zeta de Riemann — ζ(s) en el plano complejo. El color de un punto s codifica el valor de ζ(s): Colores fuertes denotan valores cercanos a 0 y el tono codifica el valor del argumento. El punto blanco en s=1 es el polo de la función zeta; los puntos negros en el eje …   Wikipedia Español

  • Función divisor — σ0(n) representada hasta n=250. Función divis …   Wikipedia Español

  • Función elíptica — En análisis complejo, una función elíptica es, hablando toscamente, una función definida sobre el plano complejo y periódica en ambas direcciones. Las funciones elípticas pueden ser vistas como generalizaciones de las funciones trigonométricas… …   Wikipedia Español

  • Función theta — En matemática, las funciones theta o θ funciones son funciones especiales de varias variables complejas. Son importantes en diversas áreas, incluidas las teorías de variedades abelianas y espacios móduli, y de las formas cuadráticas. También se… …   Wikipedia Español

  • Función gamma inversa — Gráfica de 1/Γ(x) a lo largo del eje real. Función gamma invers …   Wikipedia Español

  • Función continua — En matemáticas, una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función. Si la función no es continua, se dice que es discontinua. Generalmente… …   Wikipedia Español

  • Función zeta — Representación gráfica de la función Zeta de Riemann. Una función zeta es una función formada por una suma de infinitas potencias, o sea que se puede expresar mediante una Serie de Dirichlet: Ejemplos Existen varias …   Wikipedia Español

  • Función poligamma — Diferentes gráficas de la función poligamma a lo largo del eje x. En naranja, para m=0, en amarillo, para m=1, en verde, para m=2, en rojo, para m=3 y en azul para m=4. En matemática, la función poligamma de orden m se define como la m ésima… …   Wikipedia Español

  • Funciones elípticas de Weierstrass — Símbolo de la función P de Weierstrass P. En el ámbito de las matemáticas, las funciones elípticas de Weierstrass son un grupo de funciones elípticas que poseen una forma particularmente simple (cf funciones elípticas de Jacobi); han sido… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”