Criterio de Euler

Criterio de Euler

Criterio de Euler

En Matemáticas, el criterio de Euler es utilizado para calcular residuos cuadráticos

Definición

Sea p > 2 un número primo. Entonces x es un residuo cuadrático módulo p si y sólo si

x^{(p-1)/2} \equiv 1 \pmod p

Demostración

Primer, suponemos que 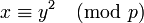x \equiv y^2 \pmod p. Se sabe por el pequeño teorema de Fermat que si p es primo, entonces 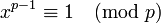x^{p-1} \equiv 1 \pmod p . Luego tenemos

x(p − 1) / 2 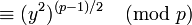\equiv (y^2)^{(p-1)/2} \pmod p
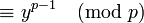
\equiv y^{p-1} \pmod p
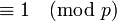
\equiv 1 \pmod p

A la inversa, suponemos que 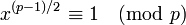x^{(p-1)/2} \equiv 1 \pmod p. Sea b un elemento primitivo modulo p. Entonces 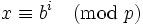x \equiv b^i \pmod p para algún i. Entonces tenemos

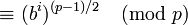
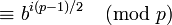
x(p − 1) / 2 \equiv (b^i)^{(p-1)/2} \pmod p
\equiv b^{i(p-1)/2} \pmod p

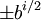Como b es de orden p-1, debe darse el caso que p-1 divide a i(p-1)/2. Por lo tanto, i es par, y las raíces cuadradas de x son \pm b^{i/2}

Obtenido de "Criterio de Euler"

Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Criterio — Saltar a navegación, búsqueda Wikcionario Wikcionario tiene definiciones para criterio. Un criterio es una condición/regla que permite realizar una elección, lo que implica que sobre un criterio se pueda basar una decisión o un juicio …   Wikipedia Español

  • Test de primalidad — El 39º número primo de Mersenne era el mayor conocido hasta la fecha de creación de este artículo. La cuestión de la determinación de si un número n …   Wikipedia Español

  • Aritmética modular — Saltar a navegación, búsqueda Cubierta de la edición original de Disquisitiones arithmeticae de Gauss, libro fundamental de la aritmética modular. En matemática, la aritmética modular es un sistema aritmético para clases de equivalencia((Clase de …   Wikipedia Español

  • Ley de reciprocidad cuadrática — En matemática, dentro de la teoría de números la ley de reciprocidad cuadrática designa al teorema áureo que relaciona la solubilidad de dos congruencias de segundo grado relacionadas: donde p y q son números primos impares.[1] …   Wikipedia Español

  • Complejidad y criptografía — La criptografía es la ciencia encargada del estudio y diseño de sistemas que permiten ocultar información. Desde sus inicios, esta capacidad de encubrimiento se ha basado en la dificultad que supondría a una entidad no autorizada el obtener la… …   Wikipedia Español

  • Test de Pépin — En matemáticas, el test de Pépin (por el matemático francés P. Pépin) es un test de primalidad que se puede emplear para determinar si un número de Fermat es primo. Es una variante del test de Proth. Contenido 1 Descripción del test 2… …   Wikipedia Español

  • Triángulo — Para otros usos de este término, véase Triángulo (desambiguación). El triángulo es un polígono de tres lados. Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran… …   Wikipedia Español

  • Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención …   Wikipedia Español

  • Problema de Basilea — Saltar a navegación, búsqueda El Problema de Basilea es un famoso problema de teoría de números, planteado por primera vez por Pietro Mengoli, y resuelto por Leonhard Euler en 1735. Puesto que el problema había resistido los ataques de los… …   Wikipedia Español

  • Historia de la geometría — La geometría es una de las más antiguas ciencias. Inicialmente, constituía un cuerpo de conocimientos prácticos en relación con las longitudes, áreas y volúmenes. En el Antiguo Egipto estaba muy desarrollada, según los textos de Heródoto,… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”